互相垂直直線的斜率乘積

互相垂直的兩直線的斜率乘積

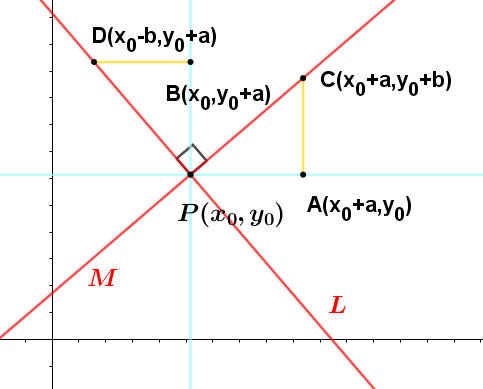
直線L和直線M垂直，而且相交於P(x₀，y₀)。

如果直線M的斜率是$\dfrac{b}{a}$，取A(x₀+a,y₀)，AC平行於y軸且交直線M於C點，則C(x₀+a,y₀+b)。

以P點為中心，將A點逆時鐘旋轉90°到B點，則B(x₀，y₀+a)。同時，C點逆時鐘旋轉90°到D(x₀-b，y₀+a)。

因此，直線L的斜率$=\dfrac{(y_0+a)-y_0}{(x_0-b)-x_0}=-\dfrac{a}{b}$。

因為線M的斜率是$\dfrac{b}{a}$，直線L的斜率$是-\dfrac{a}{b}$，所以兩直線L和M的斜率乘積等於 -1。