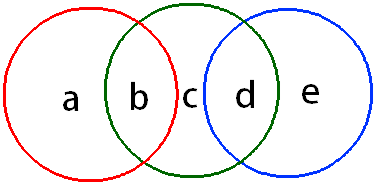
三連扣環

將1、2、3、4、5五個數全部填入三連扣環內，使得每一個環內的數字和都相等，也就是說，a+b=b+c+d=d+e。

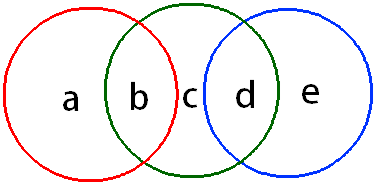
已知 a+b+c+d+e=1+2+3+4+5=15，且a=c+d，e=b+c，因此2( b+c+d )+c=15。

因為2( b+c+d )是偶數且15是奇數，所以c是奇數，c的可能值有1、3、5。

如果c=1，則b+d=6。(b，d)=(2，4)或(b，d)=(4，2)。

a	b	c	d	e
5	2	1	4	3

a	b	c	d	e
3	4	1	2	5

如果c=3，則b+d=3。(b，d)=(1，2)或(b，d)=(2，1)。

a	b	c	d	e
5	1	3	2	4

a	b	c	d	e
4	2	3	1	5

如果c=5，則b+d=0，不存在。