三角函數的和差角公式

和角公式︰

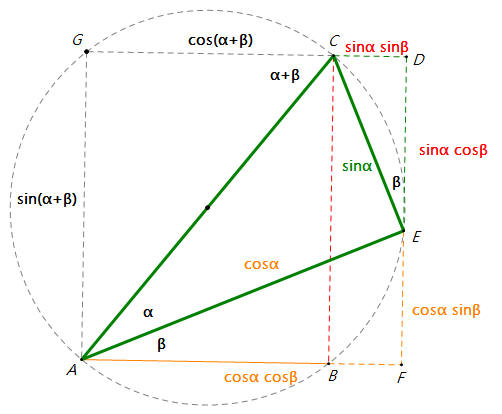
下圖，圓直徑 AC=1，∠ABC=∠AEC=∠AFE=∠CDE=∠AGC=90°，且D、E、F三點在同一直線。
∠CAE=α，∠EAF=∠CED=β，∠ACG=α+β。
CE=sinα，AE=cosα；
CD=sinα sinβ，DE=sinα cosβ；
AF=cosα cosβ，EF=cosα sinβ；
AG=sin(α+β)=DF=DE+EF=sinα cosβ+cosα sinβ。
GC=cos(α+β)=AB=AF-BF=AF-CD= cosα cosβ-sinα sinβ。
所以sin(α+β)=sinα cosβ+cosα sinβ 且 cos(α+β)=cosα cosβ-sinα sinβ。

差角公式︰

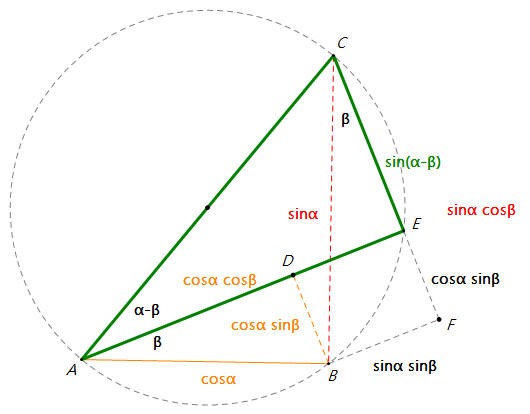
下圖，圓直徑 AC=1，∠ABC=∠AEC=∠BDE=∠EFB=90°，，且C、E、F三點在同一直線。
∠CAB=α，∠EAB=∠BCF=β，∠CAE=α-β。
CB=sinα，AB=cosα，CE=sin(α-β)；
BD=cosα sinβ=EF，AD=cosα cosβ；
BF=sinα sinβ，
CF=sinα cosβ=CE+EF=sin(α-β)+cosα sinβ。
AE=cos(α-β)=AD+DE=AD+BF=cosα cosβ+sinα sinβ。
所以sin(α-β)=sinα cosβ-cosα sinβ 且cos(α-β)=cosα cosβ+sinα sinβ。