|
|
|
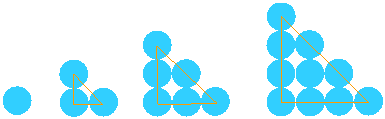
Tn-1+ Tn = (n−1)(n−1+1)2+n(n+1)2=n(n−1+n+1)2=2n22=n2
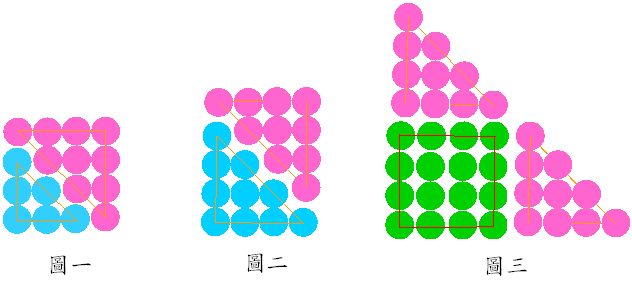
圖二,2T4
= 4
× 5,推廣可得2Tn = n(n+1)。
|
|
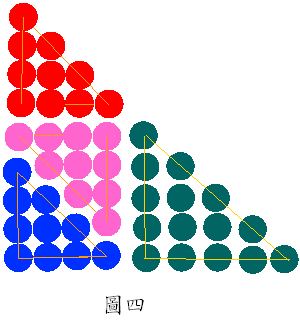
圖四,是
T2×4+1=3T4+T5,推廣可得T2n+1=3Tn+Tn+1。 3Tn+Tn+1=3n(n+1)2+(n+1)(n+2)2=(n+1)3n+n+22 = (n+1)(2n+1)。
可推廣得下列關係式: 2. 如果 n > m ,則 Tm + Tn = Tn-m + m(n+1)
|