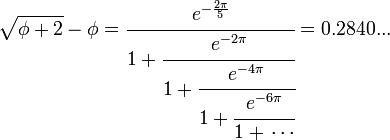
其中Φ是黃金分割比值$\frac{1+\sqrt 5}{2}$。
計程車數
英國數學家哈代(G. H. Hardy)是這樣看印度數學家拉馬努金(S. Ramanujan)的，「他在某些知識上的缺陷如同他所創造的知識一樣令人吃驚。這是一個能夠發現模形式(數論範疇)和定理的人……，他對連分數的掌握……超越任何一個數學家，他發現了ζ函數的泛函方程和解析數論中的很多著名問題的主導項。但是他卻沒有聽過雙周期函數或者柯西定理，對複變函數也只有模糊的概念............... 」
自古文人相輕，這兩人卻是惺惺相惜，二十世紀最美麗的數學界故事是這樣開始的，1913年拉馬努金寫了一封長達數頁的信件分別寄給三位英國劍橋學者貝克(H.
F. Baker)、霍布森(E. W. Hobson)和哈代，信中有許多複雜的公式，但是只有哈代注意到這位年僅23歲年輕人展現的直覺數感。
拉馬努金寄給哈代的信件︰「尊敬的先生，謹自我介紹如下，我是馬德拉斯港務信託處的一個職員，年薪只有20英鎊，23歲，我沒有接受過大學教育，可是已完成普通中學課程，在離開學校後我仍利用閒暇時間研究數學，我自修學習大學課程，並用自己的方式，對一般的發散級數做了深入的研究，本地的數學家們說，我所得到的結果是令人驚奇的...............」
哈代讀著遠從8000公里外的一個沒有接受過大學教育的南印度數學喜好者的突兀來信，哈代和他的同事利特爾伍德(J.E.
Littlewood)認真檢核過拉馬努金的公式，發現有些公式的確是前所未見，後來哈代推薦拉馬努金進到劍橋大學學習。
拉馬努金的公式裡經常出現無窮級數或連分數，例如
$\large\frac{1}{\pi}$=$\frac{2
\sqrt2}{99^2}\sum\limits_{k=0}^{\infty}\frac{(4k)!}{k!^4}$$\large\frac{26390k+1103}{396^{4k}}$
其中Φ是黃金分割比值$\frac{1+\sqrt 5}{2}$。
傳說有一次拉馬努金生病住院了，哈代搭乘計程車去探病， 並開玩笑的說︰「剛才搭車牌號碼是1729的計程車來，希望1729不是不祥的數字。」拉馬努金隨即展現其數感天賦說︰ 「1729是一 個有趣的數，它是能用兩種方法表示為兩個立方數和的最小整數。」也就是說 1729=13+123=93+103。 其實，西元1657年貝斯(B. F. de Bessy) 就發現過這個數。
後人將可用n個不同的方法表示成兩個正立方數和的整數稱做第n個計程車數(Taxicab number)，一般寫作Ta(n)或Taxicab(n)。至目前只尋找到6個計程車數，在2008年找到Ta(6)。
Ta(1) = 2 =
13+13
Ta(2) = 1729 =
13+123 =
93+103
Ta(3) = 87539319 =
1673+4363 =
2283+4233 =
2553+4143
Ta(4) = 6963472309248 =
24213+190833 =
54363+189483 =
102003+180723 =
133223+166303
Ta(5) = 48988659276962496 =
387873+3657573 =
1078393+3627533 =
2052923+3429523 =
2214243+3365883 =
2315183+3319543
Ta(6)=24153319581254312065344 =
289062063+5821623 =
288948033+30641733 =
286574873+85192813 =
270932083+162180683 =
265904523+174924963=262243663+1 82899223
Copyright © 昌爸工作坊 all rights reserved.