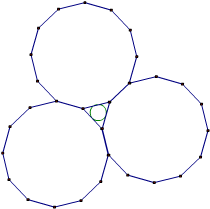
| 小明有一些大小相同的正五邊形,他用下列方式將正五邊形擺放在一圓周上,如右圖所示 (1) 每個正五邊形與相鄰的正五邊形皆有一邊緊密放在一起 (2) 每一個正五邊形皆有一邊與圓相切 若這些正五邊形正好將此圓全部圍住,則這些正五邊形最少有幾個? ans:10 |
|
團團圍住--基測題(94)
94年第二次國中基測數學第15題
| 小明有一些大小相同的正五邊形,他用下列方式將正五邊形擺放在一圓周上,如右圖所示 (1) 每個正五邊形與相鄰的正五邊形皆有一邊緊密放在一起 (2) 每一個正五邊形皆有一邊與圓相切 若這些正五邊形正好將此圓全部圍住,則這些正五邊形最少有幾個? ans:10 |
|
題目要求「正五邊形最少有幾個?」表示這些正五邊形是不重疊的全等正五邊形。
滿足條件(1)(2)的圓,其外切正n邊形的內角是 360−180(5−2)5×2= 7205(度),
所以圓外切正n邊形的每一個外角都是(180−7205)度=36度,因此n=36036=10,
因此滿足條件(1)(2)的正五邊形有10個。
試題的正5邊形只能換成正6邊形、正8邊形或是正12邊形,否則題目無解。
|
|
正8邊形 |
 正12邊形 |
Copyright ©昌爸工作坊 (數學網站)all rights reserved.