三角函數的和化積公式
sin α+sin β=2 cosα−β2× sinα+β2
cos α+cos β=2 cosα−β2× cosα+β2
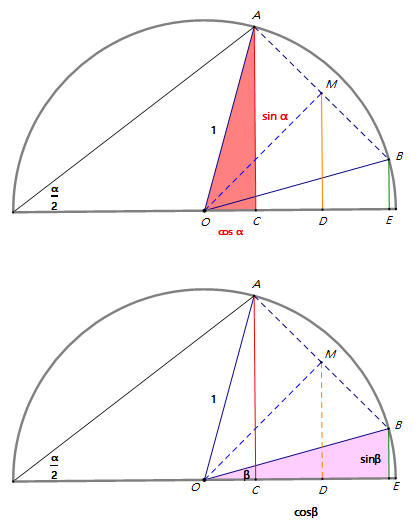
半圓半徑OA=1,∠AOE=α,∠BOE=β,OM垂直平分AB,AC⊥OE,MD⊥OE,BE⊥OE。
AC=sinα,OC=cos α;BE=sin β,OE=cos β。

OM平分∠AOB,∠AOM=α−β2,OM=cosα−β2。
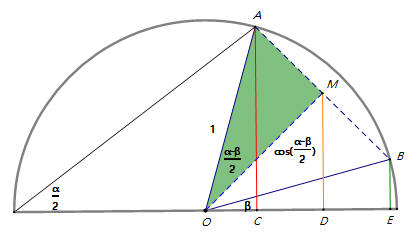
∠MOD=α−β2+β=α+β2,MD= cos α− β2× sin α+ β2 。
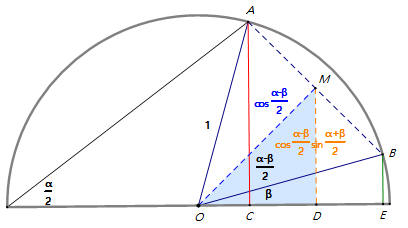
梯形ACEB,M是AB的中點,中線MD=¯AC+¯BE2=sin α+sin β2。
因為sinα+sinβ2=cosα−β2× sinα+β2 ,所以sin α+sin β=2 cosα−β2× sin α+ β2 。 ... (1)
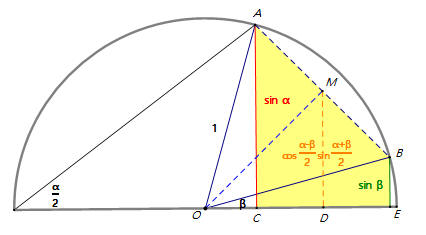
因為D是CE的中點,CD=¯OE−¯OC2=cos β−cos α2,所以OD=OC+CD=cos α+cos β−cos α2=cos β+cos α2。
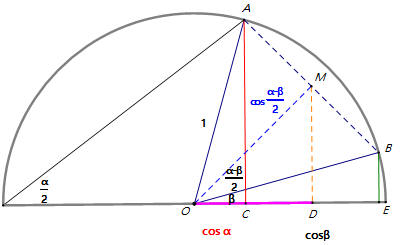
因為OD=cosα−β2 cosα+β2 ,因此 cos β+cos α2=cosα−β2 cosα+β2 ,所以cos α+cos β=2 cosα−β2× cosα+β2 。 ... (2)
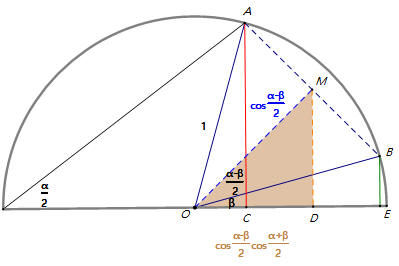
由以上圖解可知
sin α+sin β=2 cosα−β2× sinα+β2
cos α+cos β=2 cosα−β2×
cosα+β2
Copyright ©昌爸工作坊 all rights reserved.