圖說等比級數和公式

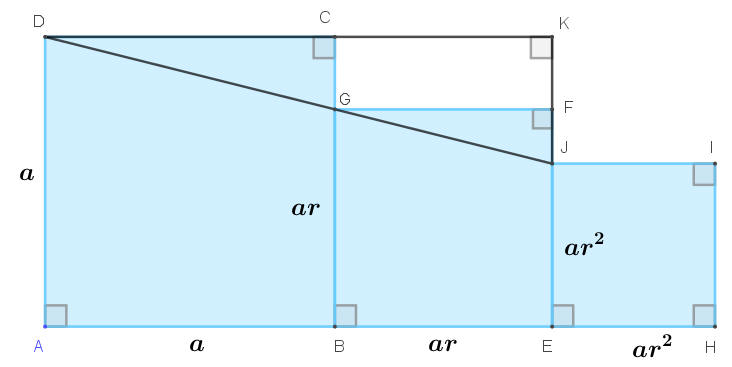
已知a>0且1>r>0，因為直角三角形DCG相似於直角三角形DKJ(AA相似)，所以DC︰DK=CG︰KJ，即 a︰a+ar=a-ar︰a-ar²，

因此 a︰a+ar=1-r︰1-r²，得 $a+ar=\dfrac{a(1-r^2)}{1-r}$。

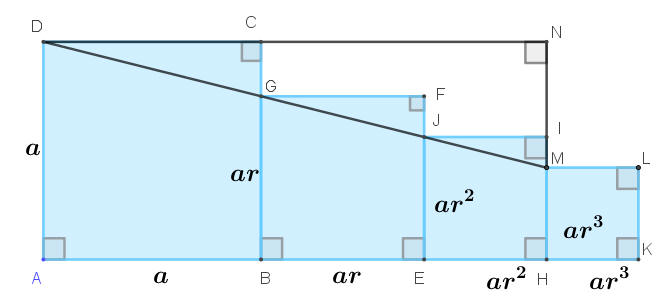
下圖，因為直角三角形DCG相似於直角三角形DNM(AA相似)，所以DC︰DN=CG︰NM，即 a︰a+ar+ar²=a-ar︰a-ar³，

因此 a︰a+ar+ar²=1-r︰1-r³，得 $a+ar+ar^2=\dfrac{a(1-r^3)}{1-r}$。

可推廣之，得 $a+ar+ar^2+\dots+ar^{n-1}=\dfrac{a(1-r^n)}{1-r}$。