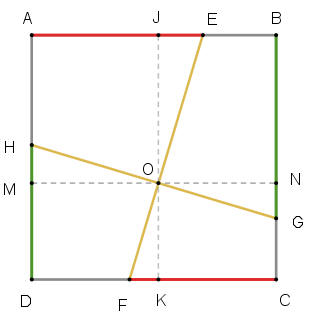
正方形內兩互相垂直線

正方形ABCD，E點在AB，F點在CD，O點在EF。過O點作EF的垂直線GH，分別和BC和AD相交於G點和H點。那麼，AE+CF=BG+DH。如果J點在AE且K點在CF，則AE+CF=(1+$\frac{\overline{FK}}{\overline{OK}}$)×AB。

過O點作JK//AD，MN//AB。
因為∠1+∠3=∠2+∠3=90°，所以∠1=∠2。
因為∠1=∠2，∠M=∠K=90°，所以直角三角形OMH相似於直角三角形OKF。
因為直角三角形OMH相似於直角三角形ONG，直角三角形OKF相似於直角三角形OJE，所以
直角三角形OMH、直角三角形ONG、直角三角形OKF、直角三角形OJE都相似。

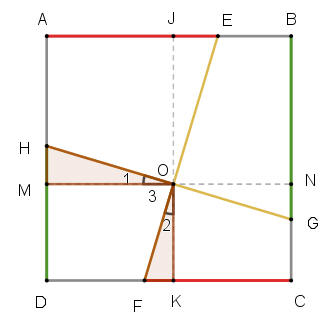
假設AB=1，OK=m，JO=1-m，MO=n，ON=1-n，J點在AE且K點在CF，FK=a。則
JE=$(\dfrac{1}{m}-1)a$，NG=$\dfrac{1}{m}(1-n)a$，HM=$\dfrac{n}{m}a$。
因為JE+FK=$(\dfrac{1}{m}-1)a$+a=$\dfrac{a}{m}$，且HM+NG=$\dfrac{n}{m}a$+$\dfrac{1}{m}(1-n)a$=$\dfrac{a}{m}$，所以JE+FK=HM+NG=$\dfrac{a}{m}$×AB。

因此AE+CF=AJ+JE+CK+FK=(AJ+CK)+JE+FK=AB+JE+FK=AB+$\dfrac{a}{m}$×AB=(1+$\frac{\overline{FK}}{\overline{OK}}$)×AB。
如果J點不在AE，則(1+$\frac{\overline{FK}}{\overline{OK}}$)×AB=2AB-(AE+CF)。