等腰三角形

等長分角線的三角形

一個14歲之前既不會讀也不會寫的人，後來成為著名射影幾何學家，發現了 Steiner 曲面 (Steiner surface) 並證明了 Poncelet-Steiner 定理，但是一道看似簡單的幾何題卻讓他，4年後才發表了定理的證明。他就是瑞士數學家思坦納(Jakob Steiner)(1796~1863)。而這一道數學題就是在西元1840年，由雷姆斯(C.Lehmus)向斯坦納(J.Steiner)提出問題：「兩個底角平分線相等的三角形是等腰三角形嗎?」。
時至今日至少超過30種的證明方法，但是思坦納(Jakob Steiner)利用反證看來簡捷易懂，仍然是最佳的證法。我參考他的證明法，些微作了一些修潤，以便學生能自學並了解。
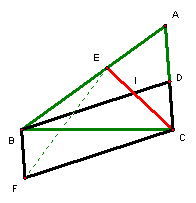
命題：「△ABC的角平分線BD=CE，則AB=AC」。
證明：

(一). 假定AB＞AC，則∠ABC＜∠ACB。...( 1 ) (大角對大邊)
(二). BD平分∠ABC，CE平分∠ACB，在△BEI與△CDI中，因為∠ABC＜∠ACB →∠EBI＜∠DCI ，又∠BIE=∠CID(對頂角相等)，所以 ∠BEI＞∠CDI(三角形內角和180∘)。...( 2 ) (三). △BDC與△CEB中，BD=CE且BC=BC，根據樞紐逆定理，因為(1)∠ABC＜∠ACB，所以BE＞CD。...( 3 )
(四). 接下來這一個巧思，成了解題的關鍵。斯坦納(J.Steiner)作了一個輔助證明的平行四邊形CDBF。並巧作輔助線 EF。 (五). 平行四邊形CDBF的對邊長相等，BF=DC。又BE＞CD...(3)，所以BE＞BF。 △BEF中，BE＞BF，所以∠2＞∠1。...(4)

(六). 因為CE=BD(已知)，BD=CF(平行四邊形對邊長相等)，所以 CE=CF，因此∠3=∠4。...(5) (七). 由(4)(5)知∠2+∠4＞∠1+∠3，也就是 ∠BFC＞∠BEC，又∠BFC=∠CDB(平行四邊形對角相等)，所以∠CDB＞∠BEC。顯然與(2)矛盾。可見假設錯誤，所以AB≯AC。 ( 八 ). 同理可證明AB≮AC。 ( 九 ) .因為AB≯AC且AB≮AC，所以AB=AC。故得證

參考連結:樞紐定理

(一). 假定AB＞AC，則∠ABC＜∠ACB。...( 1 ) (大角對大邊)
(二). BD平分∠ABC，CE平分∠ACB，在△BEI與△CDI中，因為∠ABC＜∠ACB →∠EBI＜∠DCI ，又∠BIE=∠CID(對頂角相等)，所以 ∠BEI＞∠CDI(三角形內角和180∘)。...( 2 ) (三). △BDC與△CEB中，BD=CE且BC=BC，根據樞紐逆定理，因為(1)∠ABC＜∠ACB，所以BE＞CD。...( 3 )
(四). 接下來這一個巧思，成了解題的關鍵。斯坦納(J.Steiner)作了一個輔助證明的平行四邊形CDBF。並巧作輔助線 EF。 (五). 平行四邊形CDBF的對邊長相等，BF=DC。又BE＞CD...(3)，所以BE＞BF。 △BEF中，BE＞BF，所以∠2＞∠1。...(4)

(六). 因為CE=BD(已知)，BD=CF(平行四邊形對邊長相等)，所以 CE=CF，因此∠3=∠4。...(5) (七). 由(4)(5)知∠2+∠4＞∠1+∠3，也就是 ∠BFC＞∠BEC，又∠BFC=∠CDB(平行四邊形對角相等)，所以∠CDB＞∠BEC。顯然與(2)矛盾。可見假設錯誤，所以AB≯AC。 ( 八 ). 同理可證明AB≮AC。 ( 九 ) .因為AB≯AC且AB≮AC，所以AB=AC。故得證