昌爸工作坊/探索 SSA

探索 SSA

由於SSS、SAS、ASA、AAS尺規作圖三角形的唯一性，學生透過實際操作，能輕易瞭解全等三角形。但是對於尺規作圖初學者實不宜將SSA納入教材，因為它不具備作圖的唯一性，徒增學習困擾。
很多小朋友的來信都是關於SSA的疑問，，其實，我在課堂避開不談SSA，如果學生問起，只好鼓勵有興趣的學生利用下課時間一起討論或者自行參閱下面的說明。

(1)、如果角A是直角，SSA作圖就是RHS作圖。

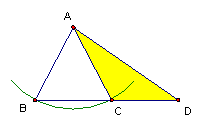
(2)、由下例可知SSA作圖不一定是全等三角形。

　

已知△ADC，∠DAC是銳角。以A點為圓心，$\overline{AC}$為半徑作圓弧交DC延長線於B點。
△ADB與△ADC中，$\overline{AD}$=$\overline{AD}$，$\overline{AB}$=$\overline{AC}$，∠D =∠D。
合乎SSA作圖，但是△ADB與△ADC不全等。

(3)、如果A是鈍角，則SSA作圖可以作全等三角形。

用反證法證明如下

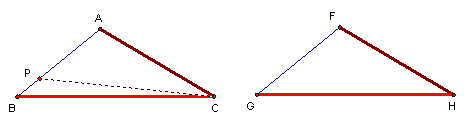
上圖，△ABC與△FGH，已知$\overline{AC}$=$\overline{FH}$，$\overline{BC}$=$\overline{GH}$，∠A=∠F > 90∘。
假設△ABC與△FGH 不全等，可令∠C > ∠H 並不失ㄧ般性。
取 ∠ACP=∠H，則△ACP△FHG (ASA) ，因此$\overline{CP}$=$\overline{HG}$ ...(1)。
已知$\overline{BC}$=$\overline{GH}$...(2)，由(1)、(2)可知$\overline{BC}$=$\overline{PC}$，由此可知△CPB是等腰△，因此∠CPB=∠CBP。
因為∠CPB是△ACP的外角，所以∠CPB > ∠A，∠CBP> ∠A > 90∘。
因為三角形的內角和是180°，由上述得知△ABC的內角∠CBP、∠A都是鈍角，而這是不可能的。
這個錯誤的結果來自錯誤的假設，既然「△ABC與△FGH不全等」的假設錯誤，那麼「△ABC與△FGH 全等」的敘述是正確的，故得證。