正方形內點分別到三頂點距離和的最小值

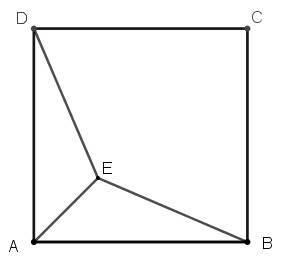
正方形ABCD內有一點E，若AB=a，則ED+EA+EB的最小值=?

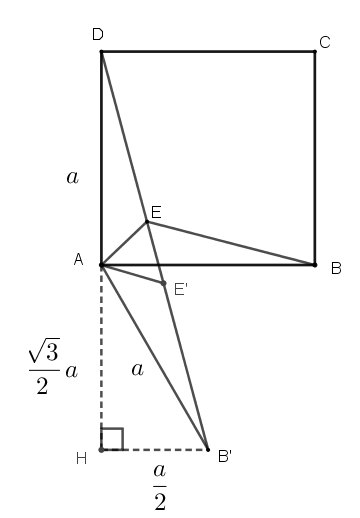
三角形ABE繞A點順時鐘旋轉60°，得三角形AB'E'，AB=AB'，AE=AE'，EB=E'B'。

因為AE=AE'且∠EAE'=60°，所以三角形AEE'是正三角形，EA=EE'。

DE+EA+EB=DE+EE'+E'B'，如果D點、E點、E' 點、點B'在一直線上，則ED+EA+EB有最小值。

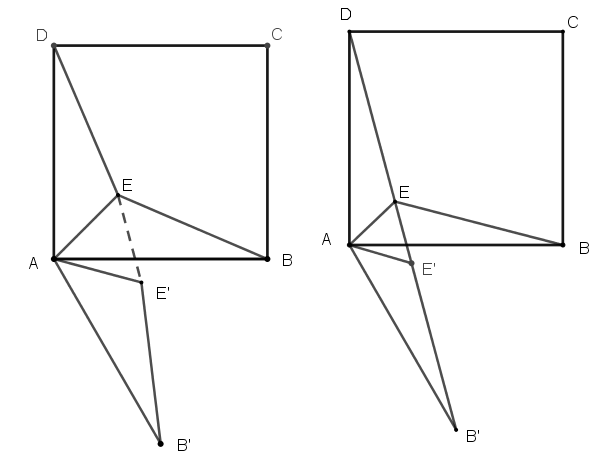
如果D點、E點、E'點、點B'在一直線上，因為DA=B'A，所以三角形DAB'是等腰三角形，∠ADB'=∠AB'D。
因為∠E'AB'=∠EAB，所以∠E'AB'+∠DAE=∠EAB+∠DAE=90°。
因此∠DAB'=∠E'AB'+∠DAE+∠EAE'=(90+60)°=150°且∠ADB'=∠AB'D=15°。

DB'=$\sqrt{(a+\frac{\sqrt{3}}{2}a)^2+(\frac{a}{2})^2}$=a$\sqrt{2+\sqrt{3}}$=$\large\frac{a}{\sqrt{2}}$$\sqrt{4+2\sqrt{3}}$=$\large\frac{a}{\sqrt{2}}$($\sqrt{3}+1$)=$\large\frac{\sqrt{6}+\sqrt{2}}{2}$a。

ED+EA+EB的最小值=$\large\frac{\sqrt{6}+\sqrt{2}}{2}$a。