sin(x+y)

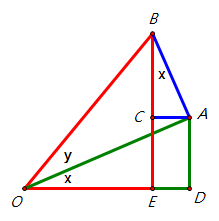
附圖，∠BEO ＝ 90^∘，∠BAO ＝ 90^∘，∠ACB ＝ 90^∘，∠ADE ＝ 90^∘。

如果∠AOD ＝ x^∘ ，∠BOA ＝ y^∘，則 ∠ABC ＝ x^∘，直角三角形BOE，sin(x+y)=$\frac{\overline{BE}}{\overline{OB}}$。

sin(x+y)=$\frac{\overline{BE}}{\overline{OB}}$=$\frac{\overline{BC}+\overline{CE}}{\overline{OB}}$=$\frac{\overline{BC}+\overline{AD}}{\overline{OB}}$=$\frac{\overline{BC}}{\overline{OB}}$+$\frac{\overline{AD}}{\overline{OB}}$=$\frac{\overline{BC}}{\overline{OB}}$×$\frac{\overline{BA}}{\overline{BA}}$+$\frac{\overline{AD}}{\overline{OB}}$×$\frac{\overline{OA}}{\overline{OA}}$=$\frac{\overline{BC}}{\overline{BA}}$×$\frac{\overline{BA}}{\overline{OB}}$+$\frac{\overline{AD}}{\overline{OA}}$×$\frac{\overline{OA}}{\overline{OB}}$=

cos x sin y+sin x cos y=sin x cos y+cos x sin y。