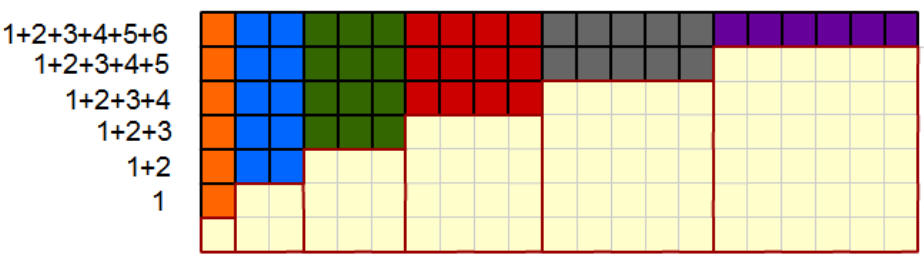
圖解 1+(1+2)+(1+2+3)+....+(1+2+3+...+n)

如圖，1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)+(1+2+3+4+5+6)的計算結果等於

寬是7且長是(1+2+3+4+5+6)的長方形面積減去6個正方形面積，這6個正方形的邊長分別是1、2、3、4、5、6。

因此，1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)+(1+2+3+4+5+6)=

(6+1)×(1+2+3+4+5+6)-(1²+2²+3²+4²+5²+6²)。

所以 1+(1+2)+(1+2+3)+(1+2+3+4)+....+(1+2+3+4+...+n)=
(n+1)(1+2+3+4+...+n)-(1²+2²+3²+4²+....+n²)=

(n+1)×$\large\frac{n(n+1)}{2}$-$\large\frac{n(n+1)(2n+1)}{6}$=$\large\frac{n(n+1)}{6}$[3(n+1)-(2n+1)]=$\large\frac{n(n+1)(n+2)}{6}$     

Copyright ©昌爸工作坊 all rights reserved.