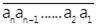 ,其中
an
> a1且
( an - a1)
×
9 =
de ,則可以速算
,其中
an
> a1且
( an - a1)
×
9 =
de ,則可以速算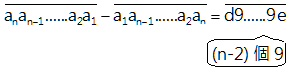 ,而其背後數學道理只是運用了退位減法。
,而其背後數學道理只是運用了退位減法。巧用退位減法速算交換首末數字差
將一個 n 位數的首位數字和末位數字交換位置得一新數,n
≧ 2,計算原數和新數的相減差(大數減小數)。如果首位數字an和末位數字a1的 n 位數記做
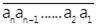 ,其中
an
> a1且
( an - a1)
×
9 =
de ,則可以速算
,其中
an
> a1且
( an - a1)
×
9 =
de ,則可以速算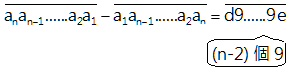 ,而其背後數學道理只是運用了退位減法。
,而其背後數學道理只是運用了退位減法。
可以這樣計算 (1) 75 - 57 =( 7 - 5 )
× 9 = 18 。(2) 82 - 28 = ( 8 - 2 )
× 9 = 54。但是為什麼呢?理由如下
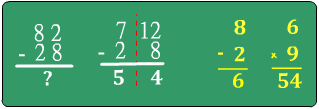
將十位數字是 a,個位數字是 b的二位數記做 ab 。如果 a > b,則 ab - ba =( 10a + b ) - ( 10b + a ) = [( 10 + b ) - a] + [ 10(a-1) - 10b ] = 10 - ( a - b ) + [ 10(a-b) -10 ] = 9( a - b )。
如何速算 572 - 275=?
先計算 ( 5-2 ) × 9 = 27,
所以 572 - 275 = 297 , 首末位數字分別是2、7,中間是9。為什麼可以這樣計算呢?理由如下
如果 x 是一位數正整數,則 9x = ( 10 - 1 )x = 10x - x = 10( x - 1 ) + ( 10 - x ),因為 9x 的十位數字是 ( x - 1 ),個位數字是 ( 10 - x ),所以 9x 的數字和是 (x-1)+(10-x) = 9。
將百位數字是 a,十位數字是 b,個位數字 c 的三位數記做 abc 。如果 a > c,且 ( a - c ) × 9 = de 則 速算 abc - cba 得 d9e ,其中 d + e = 9。
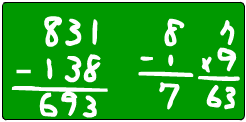
abc - cba =( 100a + 10b + c ) - ( 100c + 10b + a ) = [( 10 + c ) - a ] + [ 100 + 10(b-1) - 10b ] + [ 100( a - 1 ) - 100c ] = 99( a - c ) = 11 × 9( a - c ) =10 × de + de =de0 + de = d(e+d)e = d9e 。
可以推廣得知,如果 an
> a1,且
( an
- a1 )
× 9 = de
,n ≧ 2,則 n位數
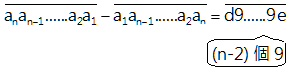 。
。
例如:
5位數 81152 - 21158 = 59994 ,其中 (8-2) × 9 = 54,並連續有 (5-2)個 9 。
7位數 6920173 - 3920176 = 2999997,其中 (6-3) × 9 = 27,並連續有 (7-2)個 9 。
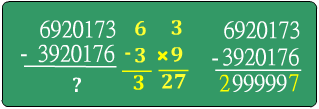
Copyright © 昌爸工作坊 All Rights Reserved.