|
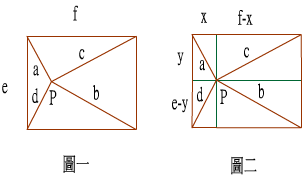
(圖一),已知P點在矩形邊上或內部,P點到各頂點的距離分別是 a、b、c、d,則 a2 + b2 + c2 + d2 的最小值和最大值分別是多少? (圖二),過P點分別做矩形長寬的平行線,0 ≦ x ≦ f, 0 ≦ y ≦ e且 a2= x2 + y2 , b2= (f - x)2 + (e - y)2 , c2= (f - x)2 + y2 , d2= x2 + (e - y)2 ,
|
|
|
a2+ b2 + c2 + d2 = 2 [ x2 + y2 + (f - x)2 + (e - y)2 ] = (f - 2x)2 + (e - 2y)2 + (e2 + f2) ≧ e2 + f2 ...(1) 因為 0 ≦ x ≦ f, -2f ≦ -2 x ≦ 0, -f ≦ f - 2 x ≦ f,所以 ( f - 2 x)2 ≦ f2 同理, ( e - 2 y)2 ≦ e2 因此 a2 + b2 + c2 + d2 = (f - 2x)2 + (e - 2y)2 + (e2 + f2) ≦ 2( e2 + f2 ) ...(2) 綜合上述(1)(2)可知 a2 + b2 + c2 + d2 的 最小值 = e2 + f2 最大值 = 2 ( e2 + f2 ) 也就是說 P點是矩形對角線交點時, P點到各頂點距離的平方和最小。 P點是矩形頂點時, P點到各頂點距離的平方和最大。 |
|