巧看循環小數 (2)
17=0.¯142857,
117=0.¯0588235294117647,
119=0.¯052631578947368421,
123=0.¯0434782608695652173913,
129=0.¯0344827586206896551724137931,
147=0.¯0212765957446808510638297872340425531914893617,
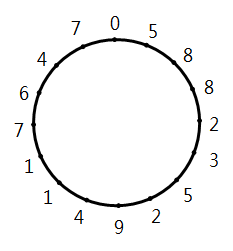
上列單位分數1P 分別乘以2、3、......、(P-1),都是循環小數,其循環節是1P的循環節的旋轉排列,例如
117=0.¯0588235294117647,217=0.¯1176470588235294,317=0.¯1764705882352941,
417=0.¯2352941176470588,517=0.¯2941176470588235,617=0.¯3529411764705882,
717=0.¯4117647058823529,817=0.¯4705882352941176,917=0.¯5294117647058823,
1017=0.¯5882352941176470,1117=0.¯6470588235294117,1217=0.¯7058823529411764,
1317=0.¯7647058823529411,1417=0.¯8235294117647058,1517=0.¯8823529411764705,
1617=0.¯9411764705882352,
其循環節是0588235294117647的旋轉排列,如圖。

有相同性質的單位分數 1P,500以內的P值就有 7、17、19、23、29、47、59、61、97、109、113、131、、149、167、179、181、193、223、229、233、263、269、313、337、367、379、383、389、419、433、461、487、491、499。
將1n化為小數(n是正整數),如果是循環小數,並分別乘以1、2、3、......、(n-1)後仍然是循環小數,則將它們的循環節依序由上而下排列,可得一個(n−1)×(n−1)的方陣,其中每行各數的相加和等於每列各數的相加和,可是不一定等於對角線各數的相加和。
W.
S. Andrews 卻發現一個數,1917年發表在他的著作《Magic Squares and Cubes》的第176頁,a19=0.¯052631578947368421×a,a=1~18,取其循環節構成18×18的方陣,在方陣中每行各數相加和等於每列各數相加和,並且等於對角線各數相加和,如圖的每行每列與對角線的各數相加和都是81。
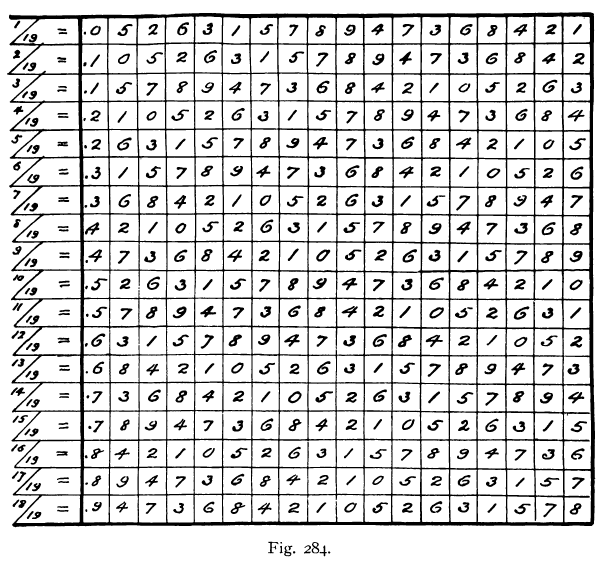
圖摘錄自《Magic Squares and Cubes》
Copyright ©昌爸工作坊 all rights reserved.