斐波拉契數列與畢氏定理

斐波拉契數列和畢氏數組

如果 m和n都是正整數且m > n，則 m²- n²、2mn、m²+n²就是畢氏數組，這是因為(m²- n²)²⁺(2mn)²=( m²+n²)²。
斐波拉契數列 1，1，2，3，5，8，13，......，如果斐波拉契數列的第x項 f_x是 a，第x+1項 f_x+1是 b，則第x+2項 f_x+2是 a+b，第x+3項 f_x+3是 a+2b。
如果 m=a+b，n=b，則 m²-n²=(a+b)²-b²=a²+2ab=a(a+2b)=f_xf_x+3。2mn=2(a+b)b=2 f_x+1 f_x+2。m²+n²=(a+b)²+b²=(f_x+2)²+(f_x+1)²。
斐波拉契數列中，第x項 f_x，則 f_xf_x+3、2 f_x+1 f_x+2、(f_x+1)²+(f_x+2)² 是畢氏數組^。

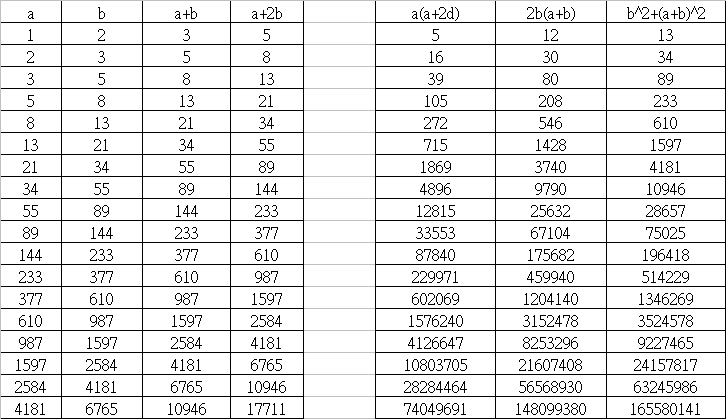
附表左，每一列的4個數是斐波拉契數列中連續4項，附表右是對應的畢氏數組。