從一道黑板習題談起

俄羅斯畫家Nikolay Bogdanov-Belsky 於1895年完成一幅畫作 〈Mental Arithmetic. In Public School of S. A. Rachinsky〉，畫中一處有一塊黑板，寫了一道計算題︰   $$\dfrac{10^2+11^2+12^2+13^2+14^2}{365}= ?$$

圖引用自Wikimedia Commons

首先，以下列方法圖解 $3^2+4^2=5^2$。

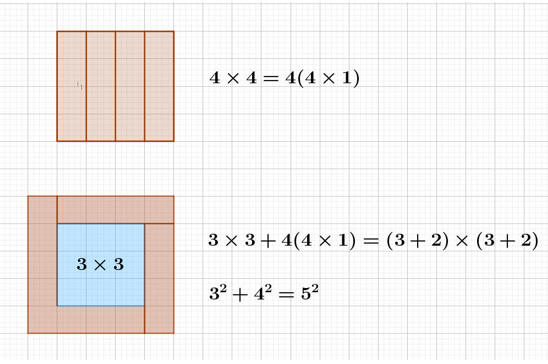
依循上述方法，

[ 10²+(12×2)×4 ]+[ 11²+(12×1)×4 ] = 13²+14² ，(如下圖)。

又 10²+(12×2)×4 ]+[ 11²+(12×1)×4 ] = 10²+11²+12×(8+4) = 10²+11²+12^{2 。}

所以 10²+11²+12²  =  13²+14² 。

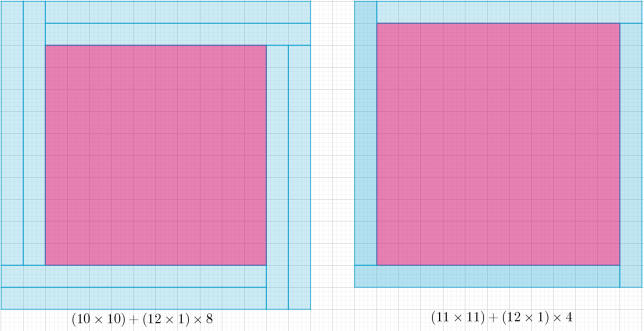
因此，圖畫裡的題解是$10^2+11^2+12^2=13^2+14^2=365$，所以$\dfrac{10^2+11^2+12^2+13^2+14^2}{365}=2$。

可以推廣得知，「若Tn=1+2+3+...+n，則 (4T_n-n)²+(4T_n-n+1)²+....+(4T_n)²=(4T_n+1)²+(4T_n+2)²+....+(4T_n+n)² 。」

例如： 若T₃=1+2+3=6，則 (4T₃-3)²+(4T₃-2)²+(4T₃-1)²+(4T₃)²=(4T₃+1)²+(4T₃+2)²+(4T_n+3)² 。

即 21²+22²+23²+24²=25²+26²+27^{2 。}

「若Tn=1+2+3+...+n，則 (4T_n-n)²+(4T_n-n+1)²+....+(4T_n)²=(4T_n+1)²+(4T_n+2)²+....+(4T_n+n)² 。」