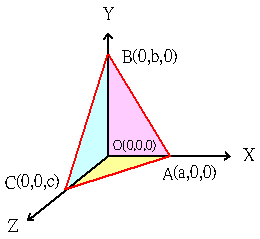
三維畢氏定理
如果你在三維直角座標系的X，Y，Z軸的正向上分別取三點A(a,0,0)，B(0,b,0)，C(0,0,c)，那麼四面體的四個面面積有一個關係式，即(△ABC面積)2=(△AOB面積)2+(△COB面積)2+(△AOC面積)2，這關係式與二維直角座標系直角三角形的畢氏定理:斜邊2=股2+股2相似，可以視(△ABC面積)2=(△AOB面積)2+(△COB面積)2+(△AOC面積)2為三維直角座標系的畢氏定理。
直角△AOB面積=
ab，△COB面積=cb，△AOC面積=ac。
△ABC的AB長=
，BC長=
，CA長=
，
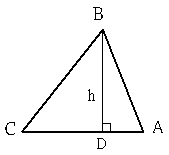
令CD長=x，則AD長是-x，如此，BC2-CD2=BA2-AD2，()2-x2=()2-(-x)2，
化簡後得
x=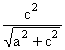
。
由畢氏定理知△BCD的BD邊長h=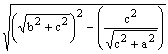
=
，所以△ABC面積==
。
因此，(△ABC面積)2=(△AOB面積)2+(△COB面積)2+(△AOC面積)2。
Copyright ©昌爸工作坊 all rights reserved.