厄拉多塞篩法

質數是只有兩個正因數，是1和它自己。所以質數不能表示為比它小的數字的乘積。
西元前250年，希臘數學家厄拉多塞(Eeatosthese)提出質數篩法，降低逐一檢查每個數的的步驟，用比較簡單的方法從一大堆數字中篩選出質數來，這方法被稱作厄拉多塞篩法(Sieve of Eeatosthese)。

以找出1~50之間的質數為例

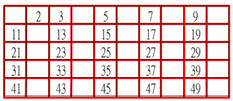
2是質數，以2為篩子，留下2並刪去2的倍數。

2之後未被刪去的第一個數是3，它是質數。以3為篩子，留下3並刪去3的倍數。

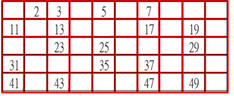
3之後未被刪去的第一個數是5，它是質數。以5為篩子，留下5並刪去5的倍數。

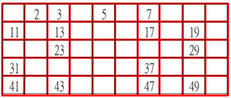
5之後未被刪去的第一個數是7，它是質數。以7為篩子，留下7並刪去7的倍數。

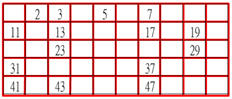
完成尋找所有介於1和50之間的質數，因為50的平方根大於7而且小於8，現在表格所剩的數字都是質數。