點到直線的距離

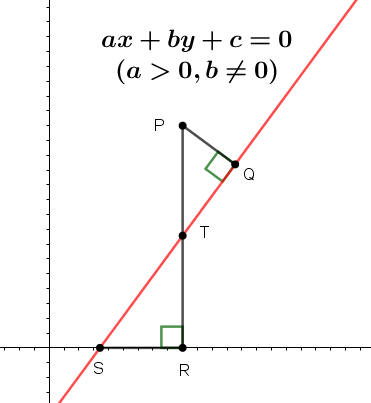
直線L方程式ax+by+c=0，a＞0，b≠0。P點(x₀，y₀)到直線L的距離為何?

考慮利用直線斜率和相似形對應邊成比例，求點到直線的距離。

PQ是P點到直線L的距離，PR平行於y軸並交L於T點。

因為直線ax+by+c=0的斜率是$-\dfrac{a}{b}$，如果SR=|-bk|=| bk |，則RT=ak，k是大於0的常數。

因為P(x₀，y₀)，T(x₀，$\dfrac{-ax_0-c}{b}$)，所以PT=|$\dfrac{by_0-(-ax_0-c)}{b}$ |=|$\dfrac{ax_0+by_0+c}{b}$ |

因為PQ︰PT=SR︰ST，所以PQ︰|$\dfrac{ax_0+by_0+c}{b}$ |=| bk |︰$\sqrt{a^2+b^2}$k=| b |︰$\sqrt{a^2+b^2}$。

因此 PQ×$\sqrt{a^2+b^2}$=|${ax_0+by_0+c}$ |，即

PQ=$\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$。

P點(x₀，y₀)到直線L︰ax+by+c=0的距離是$\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$。

Copyright © 昌爸工作坊 all rights reserved.