昌爸工作坊/達文西的素描

達文西的多面體素描

正四面體、正八面體、正二十面體的每一面都是正三角形，正方體的每一面是正方形，而正十二面體的每一面都是正五邊形。

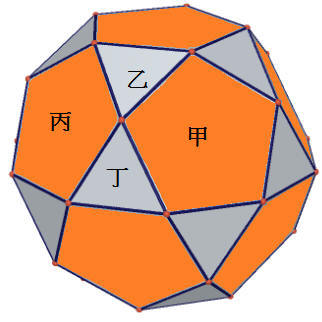
美國作家麥可‧懷特(Michael White )在他的著作《達文西：科學第一人》(Leonardo: The first scientist) 中提到達文西曾經畫過一幅封閉多面體(截半20面體)，如附圖，這個多面體由邊長一樣的正三角形與正五邊形組合而成，而且正五邊形的每邊都與正三角形共邊，正三角形的每邊也都與正五邊形共邊。那麼它應該包含有幾個正三角形和正五邊形呢？

因為多面體的頂點數 – 邊數 + 面數 = 2 (尤拉公式)，觀察附圖，不難發現甲、乙、丙、丁共用一個頂點，而且甲、乙共用一個邊。如果有a的正三角形，b個正五邊形，那麼，這個多面體就有( 3a + 5b ) ÷ 4個頂點，( 3a + 5b ) ÷ 2個邊，並且有 a + b個面。因此，( 3a + 5b ) ÷ 4 - ( 3a + 5b ) ÷ 2 + ( a + b ) = 2，即 a - b = 8 .....(1); 又因為所有正三角形的邊個數和正五邊形的邊個數是一樣的，即3a = 5b....(2)。

由(1)(2)可知 a = 20，b = 12。所以，達文西(Leonardo de Vinci)所畫的多面體，應該是20個正三角形和12個正五邊形組合而成。