等比數字方盒
連接正方形的每邊中點得一個新正方形,重複n次得n個正方形,由外而內總共有(n+1)個正方形,如附圖。
由外而內分別是第1層、第2層、第3層、...。
在第1層正方形的四個頂點各填上一個數,將相鄰兩頂點的數相減求差(大數-小數),並將此差填寫在邊上的中點上。連接4個中點成下一層正方形,循上述步驟,幾回和後會出現一層正方形,其頂點上的數字都是相同的,如此層層正方形組成的圖形稱之為數字方盒。
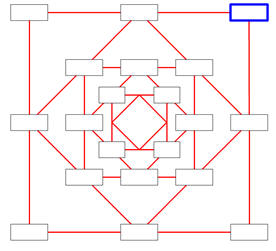
如果第1層正方形頂點填入的數依序是1、r、r2、r3成等比,r是大於1的整數,則各層正方形其頂點上的數如下:
| 第1層 | 1 | r | r2 | r3 |
| 第2層 | r-1 | r(r-1) | r2(r-1) | r3-1 |
| 第3層 | (r-1)2 | r(r-1)2 | r2-1 | r(r2-1) |
| 第4層 | (r-1)3 | ※ | (r-1)2(r+1) | (r-1)(r2+1) |
※ 如果r=2時,第4層第2個數是(r-1)(-r2+2r+1)。
※ 如果r≧3時,第4層第2個數是(r-1)(r2-2r-1)。
當r=2時,第7層正方形頂點的數都是相同的2。
| 第1層 | 1 | r | r2 | r3 |
| 第2層 | r-1 | r(r-1) | r2(r-1) | r3-1 |
| 第3層 | (r-1)2 | r(r-1)2 | r2-1 | r(r2-1) |
| 第4層 | (r-1)3 | (r-1)(-r2+2r+1) | (r-1)2(r+1) | (r-1)(r2+1) |
| 第4層 | 1 | 1 | 3 | 5 |
| 第5層 | 0 | 2 | 2 | 4 |
| 第6層 | 2 | 0 | 2 | 4 |
| 第7層 | 2 | 2 | 2 | 2 |
當r≧3時
| 第1層 | 1 | r | r2 | r3 |
| 第2層 | r-1 | r(r-1) | r2(r-1) | r3-1 |
| 第3層 | (r-1)2 | r(r-1)2 | r2-1 | r(r2-1) |
| 第4層 | (r-1)3 | (r-1)(r2-2r-1) | (r-1)2(r+1) | (r-1)(r2+1) |
| 第5層 | 2(r-1) | 2r(r-1) | 2(r-1) | 2r(r-1) |
| 第6層 | 2(r-1)2 | 2(r-1)2 | 2(r-1)2 | 2(r-1)2 |
如果第1層正方形頂點依序是1、r、r2、r3成等比,則
(1) r=1,第1層正方形頂點1、1、1、1。
(2) r=2,第7層正方形頂點2、2、2、2。
(3) r≧3,第6層正方形頂點都是2(r-1)2。
沿伸閱讀:
第34屆全國中小學科學展覽國小數學組優勝----- 數字方塊
第45屆全國中小學科學展覽國中數學組佳作----- 層出不窮?!
第50屆全國中小學科學展覽國小數學組第三名---- 數字方塊尋極限
~數字方塊擴展層數極限的探討