項鍊兩位數字和

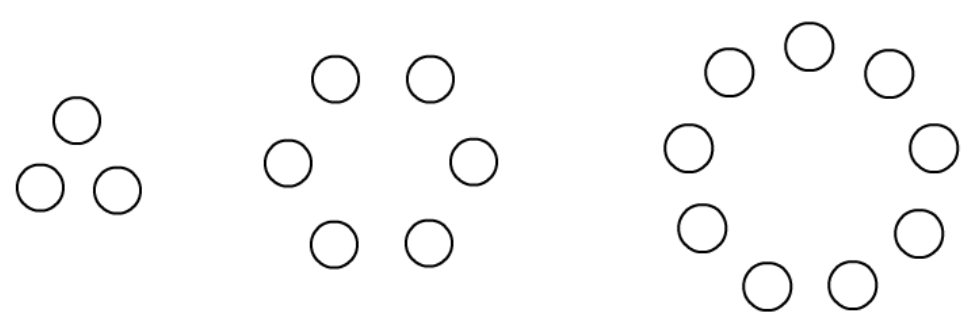
項鍊二位數字和

你可以先畫出圓圈，圓圈個數可以是2~10個，如果三個以上，請將圓圈排成環狀如項鍊，如下圖。

從0~9挑選其中幾個數填入園圈內，但是每一個數只能挑選一次。
選定其中一個圓圈開始，可以逆時鐘每相鄰兩個圓圈一組直到原來選定的圓圈為止，每一組組成一個二位數或一位數。每一組的第一個圓圈的數字當二位數的十位數，同一組的第二個圓圈的數字當二位數的個位數。如果一開始同時都依順時鐘分組也可以。

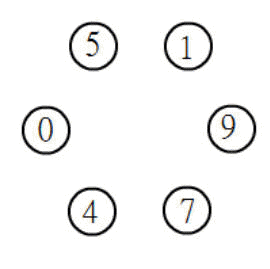
下圖，從5開始順時鐘分組，得二位數分別是51、19、97、74、40、5。將左列每一個數相加，計算51+19+97+74+40+5=286。
從5開始如果改依逆時鐘分組，得二位數分別是50、4、47、79、91、15。將左列每一個數相加，計算50+4+47+79+91+15=286。

你可以發現不論是依逆時鐘或依順時鐘，會有相同的相加和。那麼，是否其他圓圈數(2~9)的項鍊環也有一樣的結果呢?
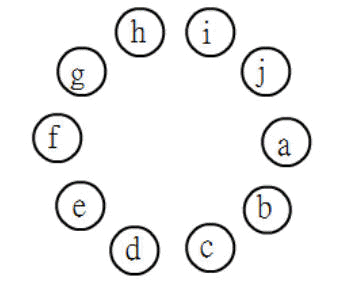
下圖，a、b、c、d、e、f、g、h、i、j，每一個數只對應0~9其中一個數，而且不重複。
如果由a開始順時鐘分組，則
(10a+b)+(10b+c)+(10c+d)+(10d+e)+(10e+f)+(10f+g)+(10g+h)+(10h+i)+(10i+j)+(10j+a)

=11(a+b+c+d+e+f+g+h+i+j)。
如果由a開始逆時鐘分組，則
(10a+j)+(10j+i)+(10i+h)+(10h+g)+(10g+f)+(10f+e)+(10e+d)+(10d+c)+(10c+b)+(10b+a)

=11(a+b+c+d+e+f+g+h+i+j)。

所以畫出2~10個圓圈，排成環狀項鍊，並在每一個圓圈填入0~9其中一個數，不可以重複取數。依上述方法取二位數或一位數並將所有數相加，則無論是逆時鐘或順時鐘，其加總和是一樣的。