連續自然數的立方和

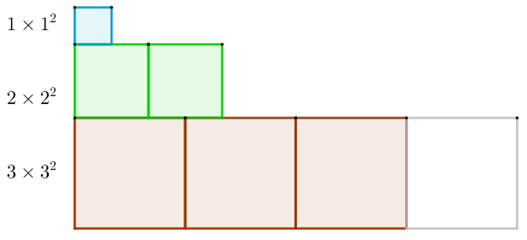
圖示連續自然數的立方和

觀察下列圖示，可知1個邊長1的正方形、2個邊長2的正方形、3個邊長3的正方形的面積總和是1×1²+2×2²+3×3²。

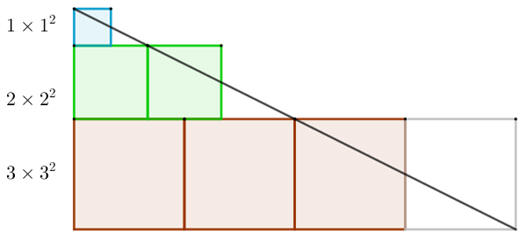
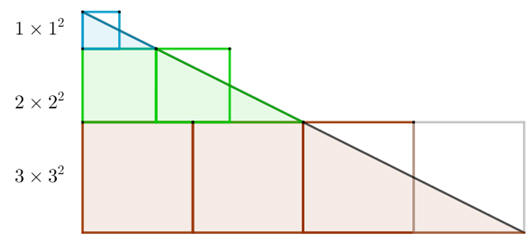
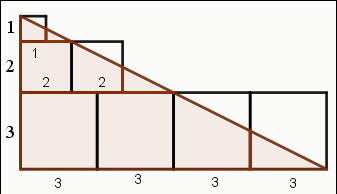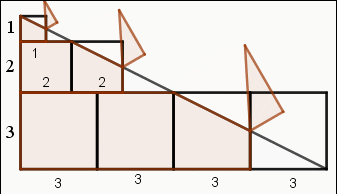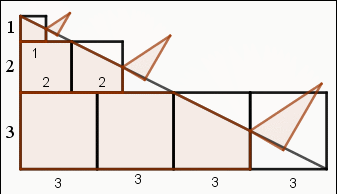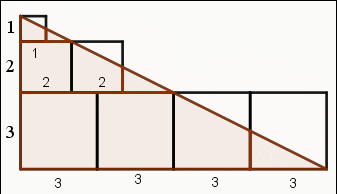
經過等積轉換成為一個兩股長分別是(1+2+3)和(4×3)的直角三角形，面積是$\large\frac{1}{2}$(1+2+3)(4×3)。

所以，1×1²+2×2²+3×3²= 1³+2³+3³ =$\large\frac{1}{2}$(1+2+3)(4×3)。

推廣知， 1×1²+2×2²+3×3²+......+n×n²= 1³+2³+3³ +......+n³= $\large\frac{1}{2}$(1+2+3+......+n)[(n+1)n]。

因此，1³+2³+3³ +......+n³= $\large\frac{1}{2}$×$\large\frac{1}{2}$[n(n+1)][(n+1)n]=$(\large\frac{n(n+1)}{2})^2$