等和三角形周邊數

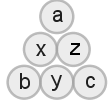
等和的三角形周邊數

三角形每一邊需填入三個數，使得每一邊的三個數相加和都相等。如果填入的數是自然數1、2、3、4、5、6，則有幾組解？( 一組解和其經過旋轉對稱或反射對稱所得到的解都視作同一組解 )

上圖，a+b+c+x+y+z=1+2+3+4+5+6=21，且 a+x+b=b+y+c=c+z+a=s，因此(a+b+c+x+y+z)+a+b+c=3s，
a+b+c=3s-21。因為 1+2+3 ≦ a+b+c ≦ 4+5+6，6 ≦ a+b+c ≦ 15，所以6 ≦ 3s-21 ≦ 15，27 ≦ 3s ≦ 36，得 9 ≦ s ≦ 12。

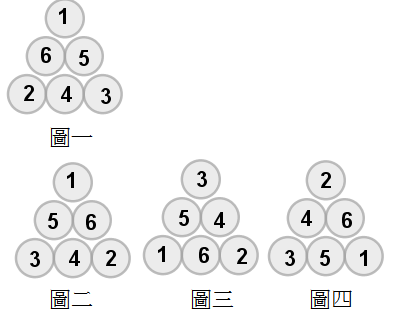
(1) 當 s=9時，圖一和圖二是反射對稱，圖一和圖三是旋轉對稱，圖一和圖四是旋轉對稱，將圖一、圖二、圖三、圖四視為同一組解。

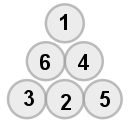
(2) 當 s=10時，

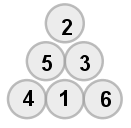
(3) 當 s=11時，

(4) 當 s=12時，

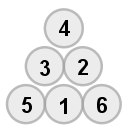
由上述可知，將1、2、3、4、5、6填入每一邊有三個數的三角形，如果每一邊的三數相加和相等，則有四組解。

相關連結：等和的三角形周邊數 ggb檔