魔方陣
傳說四千多年前夏禹治水時，在洛河浮現一隻靈龜，背殼上有神奇圖紋，後人稱作洛書。
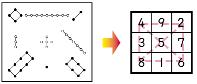
中國漢代時期，將數字1~9填入九個空格內，每一行、每一列及兩個對角線上的數字的和都是15，稱作九宮圖或三階幻方。
南宋楊輝著《續古摘奇算法》(西元1275年)中敘述三階幻方(縱橫圖)的構造方法：
「九子斜排，上下對易，左右相更，四維挺出，戴九履一，左三右七，二四為肩，六八為足」
縱橫圖就是現在的魔方陣。
金庸小說射雕英雄傳第二十九回有一段文章敘述魔方陣，
「九宮之義，法以靈龜，二四為肩，六八為足，左三右七，戴九履一，五居中央」
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
n階魔方陣中每一行、每一列、兩對角線的數字和都是$\frac{n(n^2+1)}{2}$。
理由：1 ~n2填入n階魔方陣，因為1+2+3+...+n2=$\frac{n^2(n^2+1)}{2}$，而且每一行的和都相等，因此每一行的和都是
$\large\frac{\frac{n^2(n^2+1)}{2}}{n}$=$\frac{n(n^2+1)}{2}$。
你可以試著畫4階、5階魔方陣
|
X |
X |
X |
X |
|
X |
X |
X |
X |
|
X |
X |
X |
X |
|
X |
X |
X |
X |
Copyright © 昌爸工作坊 all rights reserved.