無聲勝有聲

佛蘭克‧納爾遜‧柯爾(Frank Nelson Cole)是美國哥倫比亞大學的教授。西元1903年於紐約數學學會的會議，發表一篇題名『有關大數字的因子分解法』(On the factorisation of large numbers )的研究報告。

佛蘭克‧納爾遜‧柯爾站在講臺，沒說任何一句話，只用粉筆在黑板寫出2⁶⁷－1和193707721×761838257287 。全場卻響起如雷掌聲。這是發生甚麼事了？

原來佛蘭克‧納爾遜‧柯爾已經解決懸宕兩百年的問題，「 2⁶⁷－1 是不是質數？」

因為2⁶⁷－1=193707721×761838257287，即2⁶⁷－1 可以分解成兩個非1和本身的因數，因此證明2⁶⁷－1不是質數。

　　
雖然佛蘭克‧納爾遜‧柯爾只列一個簡短的無聲報告，卻花費他3年的時間來研究才得到這個結論。簡單算式蘊含了佛蘭克‧納爾遜‧柯爾的驚人毅力，其結果不遜於任何一篇萬言報告書。

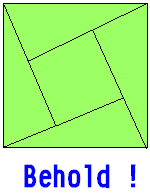
印度數學家婆什迦羅（Bhaskara，1114~1185）證明畢達哥拉斯定理的方法也是令人拍案叫絕，他只利用一張圖(如附圖)和一個字『看啊!』(BEHOLD!)。
　

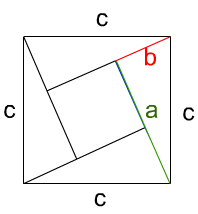
c²= 2ab+(a-b)²，得 c²=a²+b²。