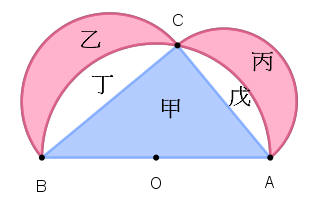
月牙面積和定理

以AB為直徑的半圓O面積=直角三角形(甲)面積+弓形(丁)面積+弓形(戊)面積。
以BC為直徑的半圓面積=弓形(丁)面積+月牙(乙)面積。
以AC為直徑的半圓面積=弓形(丙)面積+月牙(戊)面積。

因為三角形ABC的∠C是直角，所以$\overline{AB}^2$=$\overline{BC}^2$+$\overline{AC}^2$，因此$\large(\frac{1}{2})\pi(\frac{\overline{AB}}{2})^2$=$\large(\frac{1}{2})\pi(\frac{\overline{BC}}{2})^2$+$\large(\frac{1}{2})\pi(\frac{\overline{AC}}{2})^2$，

以AB為直徑的半圓O的面積等於以BC為直徑的半圓面積和以AC為直徑的半圓面積相加和。
甲+丁+戊=(乙+丁)+(丙+戊)，得甲=乙+丙，所以直角三角形ABC的面積等於月牙乙和月牙丙的面積和。

相關連結︰月牙面積和定理 (ggb)

Copyright © 昌爸工作坊 All Rights Reserved.