由餘弦定理談SSA作圖

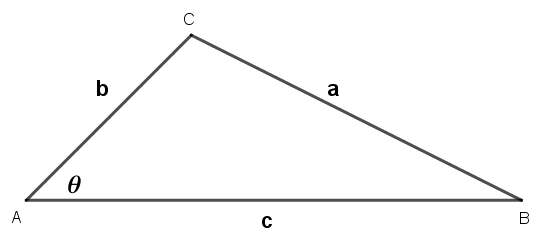
下圖，三角形ABC，BC=a，AC=b，AB=c，∠CAB=θ。已知餘弦定理 a²=b²+c²-2bc cosθ。

「SSA是否可以唯一作圖」等價於「已知a²=b²+c²-2bc cosθ的a、b、θ三數值，則未知數c值是否唯一存在。」

a²=b²+c²-2bc cosθ，得知c²-2bc cosθ+(b²-a²)=0。

平時習慣以x表示未知數c，即x²-(2b cosθ) x+(b²-a²)=0。

如果△=(2b cosθ)²-4(b²-a²) ≧ 0，則方程式x²-(2b cosθ) x+(b²-a²)=0有實數解。

(ㄧ)

方程式x²-(2b cosθ) x+(b²-a²)=0

如果△ = 0，且二重根是正數，則c值唯一存在，即可以SSA作圖。

因為(2b cosθ)²-4×1×(b²-a²)=0，即-4b²sin²θ+4a²=0，得a²=b²sin²θ，所以a=bsinθ。

因為二重根是正數，由韋達定理(Vieta's formulas)知2b cosθ > 0且b²-a²> 0，所以b > a且cosθ > 0，即 0° < θ <90°。

已知正弦定理$\dfrac{a}{sin\theta}=\dfrac{b}{sinB}$，而且a=bsinθ，所以sinB=1，即∠B=90°。

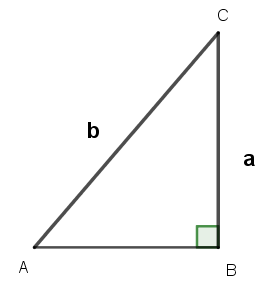
「已知一直角，兩線段長a和b，其中 a < b，則可以SSA作圖直角三角形ABC，其中BC=a，AC=b，∠CAB=90°。」

(二)

方程式x²-(2b cosθ) x+(b²-a²)=0

(1) 如果△ > 0，而且有一個正根，另一根是 0，則c值唯一存在，即可以SSA作圖。

由韋達定理(Vieta's formulas)知兩根積=b²-a²=0且兩根和=2b cosθ>0。

因此b=a且cosθ > 0，即 0° < θ <90°。

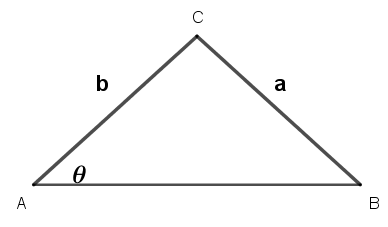
「已知一銳角θ，兩線段長a和b， a = b，則可以SSA作圖等腰三角形ABC，其中BC=a，AC=b，∠CAB=θ。」

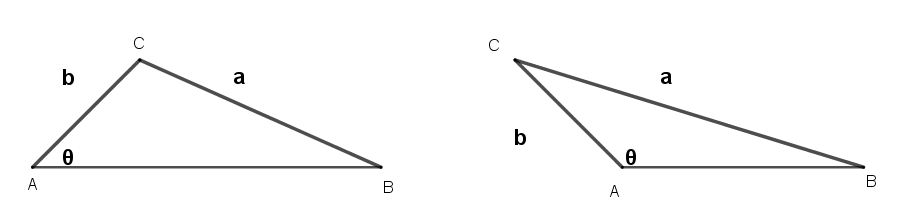
(2) 如果△ > 0，而且有一個根是正數，另一根是負數，則c值唯一存在，即可以SSA作圖。

由韋達定理(Vieta's formulas)知兩根積=b²-a²<0，即 a > b。

如果 0° < θ <90°且a > b，則c值唯一存在，即可以SSA作圖。

如果90° < θ <180°，則 a > b，因此c值唯一存在，即可以SSA作圖。

「已知一角θ不是直角，兩線段長a和b， a > b，則可以SSA作圖三角形ABC，其中BC=a，AC=b，∠CAB=θ。」