恆等式
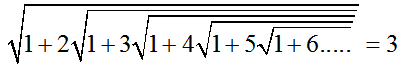
若函數f(x)=x(x+2),其中x是正整數,則f(x+1)=(x+1)(x+3)=(x+2)2-1,因此1+f(x+1)=(x+2)2,x+2=√1+f(x+1),所以f(x)=x√1+f(x+1)。
使用函數f(x)=x√1+f(x+1)迭代計算可得f(x+1)=(x+1)√1+f(x+2),
因此f(x)=x√1+(x+1)√1+f(x+2)。
因為f(x+2)=(x+2)√1+f(x+3),所以
f(x)=x√1+(x+1)√1+(x+2)√1+f(x+3)。
因為f(x+3)=(x+3)√1+f(x+4),所以
f(x)=x√1+(x+1)√1+(x+2)√1+(x+3)√1+f(x+4)。
如此迭代計算下去,可得
f(x)=x√1+(x+1)√1+(x+2)√1+(x+3)√1+(x+4)√...√1+(x+n−1)√1+f(x+n),其中n是趨向無限大的正整數。
當上列恆等式中的x=1時,f(1)=1×3=3
3=f(1)=1×√1+f(2)=1×√1+2×4
3=f(1)=1×√1+2√1+f(3)=1×√1+2√1+3×5
3=f(1)=1×√1+2√1+3√1+f(4)=1×√1+2√1+3√1+4×6
3=f(1)=1×√1+2√1+3√1+4√1+f(5)=1×√1+2√1+3√1+4√1+5×7
....................
20世紀印度數學英才拉馬努金(Ramanujan),擁有非常人的數感,具有前瞻性的洞察力,在其數學成就中就包含約4000個恆等式,但是有一些恆等式雖有結論,卻沒有留下詳細的推論過程。
本文的恆等式就是由拉馬努金(Ramanujan)所提出的。
延伸閱讀: 中山大學應數雙週一題徵答