海龍公式 Heron's formula
海龍
(Heron)（西元1-75)生於歐幾理得之後350年左右，古希臘亞歷山大里亞(Alexandria)的數學家、力學家、機械學家。海龍在他的著作《Metrica》（測量術）提出Heron's
formula的證明，我們則試著運用切線長和相似三角形來和國中三年級學生一起探索Heron's
formula。
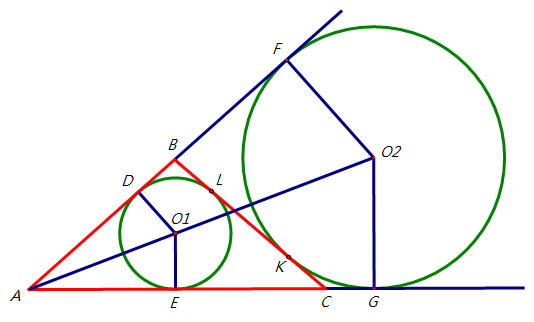
圖一，△ABC的內心是O1，傍心是O2，D、E、F、G和L、K都是切點。
在△ABC，因為AD=AE，BD=BL，CE=CL，所以△ABC的周長=2 (
AD+BL+CE )。
(圖一)
圖二，假設 BC=a，CA=b，AB=c，s=$\Large\frac{a+b+c}{2}$，則AD=AE=s-a，BD=BL=s-b，CE=CL=s-c。
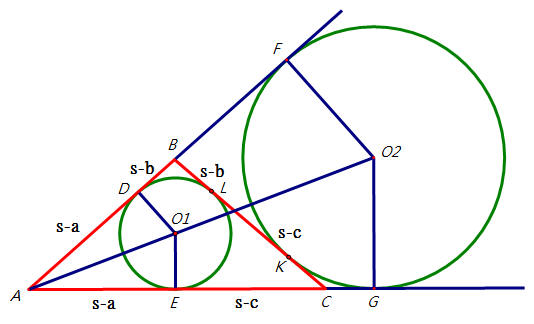
(圖二)
圖三，圓O2，BF=BK=BL+LK。
圓O1，CE=CL=CK+KL。
圓O1和圓O2，AD=AE且AF=AG，所以AF-AD=AG-AE，因此DF=EG。
因為DB+BF=BL+BK=2 DB+LK，且EC+CG=CL+CG=2 CG+LK，所以DB=CG=s-b。
因此 DF-DB=EG-CG，即 BF=EC=s-c。
因為△ADO1~△AFO2，所以 DO1:FO2=(s-a):(s-a)+(s-b)+(s-c)=(s-a):s ...(1)
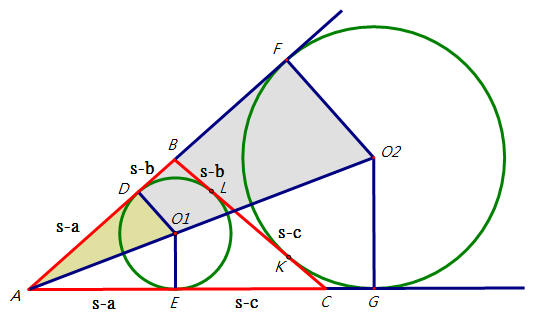
(圖三)
圖四，直角△CEO1和直角△O2GC，因為CO1平分∠BCA，且CO2平分∠BCG，所以∠O1CE=∠CO2G，
因此△CEO1~△O2GC(AA相似)。
所以EO1:GC=CE:GO2，即EO1:(s-b)=(s-c):GO2
...(2)
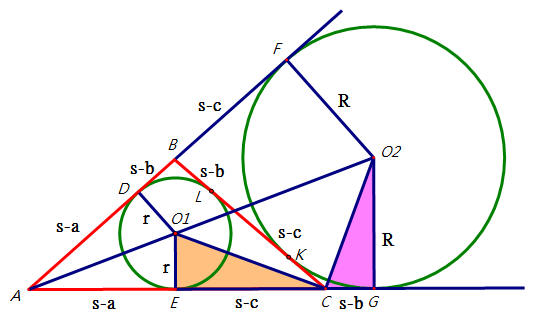
(圖四)
假設圓O1半徑=r，圓O2半徑=R，由(1)(2)可知
r:R=(s-a):s且r:(s-b)=(s-c):R，即r=$\Large\frac{R(s-a)}{s}$且rR=(s-b)(s-c)。
因此r=$\Large\frac{\frac{(s-b)(s-c)}{r}(s-a)}{s}$，得r2=$\Large\frac{(s-a)(s-b)(s-c)}{s}$，
因此(rs)2=s(s-a)(s-b)(s-c)。
所以△ABC的面積=rs=$\large\sqrt{s(s-a)(s-b)(s-c)}$，其中
s=$\Large\frac{a+b+c}{2}$。