多邊形數

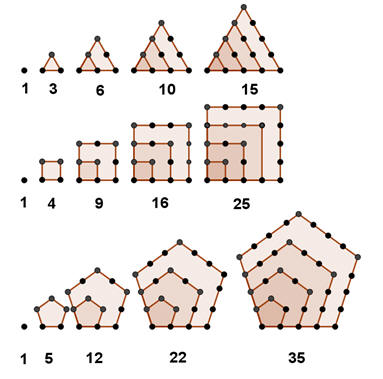
附圖，三邊形數分別是1、3、6、10、15。四邊形數分別是1、4、9、16、25。五邊形數分別是1、5、12、22、35。

觀察下列多邊形數

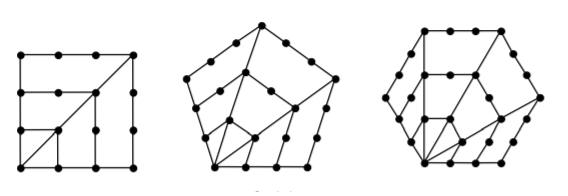
第4個四邊形數=2×(第4個三邊形數)-4，第4個五邊形數=3×(第4個三邊形數)-4×2，第4個六邊形數=4×(第4個三邊形數)-4×3。

推廣到第n個x邊形數=(x-2)×(第n個三邊形數)-(x-3)n。

因為第n個三邊形數=1+2+3+...+n=$\large\frac{n(n+1)}{2}$

所以第n個x邊形數=(x-2)×(第n個三邊形數)-(x-3)n=(x-2)×$\large\frac{n(n+1)}{2}$-(x-3)n=

(x-2)×$\large\frac{n(n+1)}{2}$-(x-2)n+n=(x-2)×$\large\frac{n(n-1)}{2}$+n，

因此，第n個x邊形數是 $\large\frac{n^2-n}{2}$(x-2)+n 。