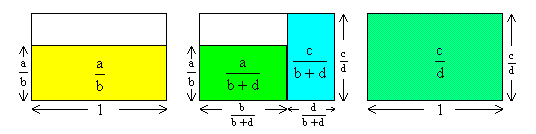
圖示ab<a+cb+d<cd
b>a>0且d>c>0,ab<cd,則如何比較 ab和cd和a+cb+d 的大小關係?
下列圖示已經可以清楚解釋其關係

也可以用代數法說明
因為ab<cd且 bd > 0,所以bd×ab < bd×cd,因此 ad < bc。
ab-a+cb+d=a(b+d)−b(a+c)b(b+d)=ad−bcb(b+d)<0,因此ab<a+cb+d。
cd-a+cb+d=c(b+d)−d(a+c)d(b+d)=cb−dab(b+d)>0,因此cd>a+cb+d。
因此ab<a+cb+d<cd。
Copyright ©昌爸工作坊 all rights reserved.