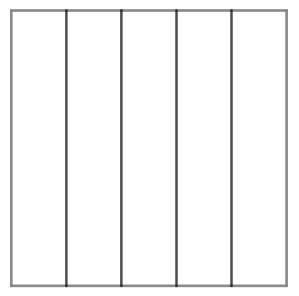
分割正方形成五個等積多邊形

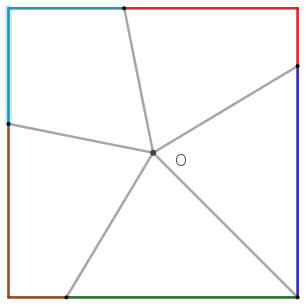
圖一，將正方形五等分成五個長方形。圖二，可參閱「過正方形中心點，五等分正方形的面積」


圖一	圖二

「下圖，取正方形ABCD的各邊中點E、F、G、H。分別連接AE、BH、CG、DF。則正方形MNKL、直角三角形ADN、直角三角形BAM、直角三角形CBL、直角三角形DCK的面積都等於正方形ABCD面積的$\dfrac{1}{5}$。」

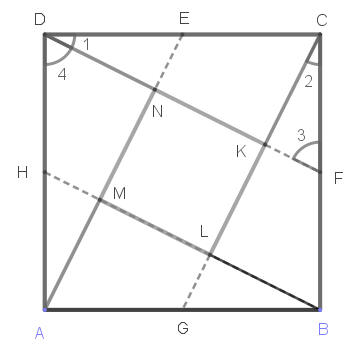
因為E、F、G、H是正方形ABCD的各邊中點，所以直角三角形ADE、直角三角形BAH、直角三角形CBG、直角三角形DCF都全等(SAS全等性質)，因此∠1=∠2。因為∠3=∠4(內錯角)，∠1+∠4=90°，所以∠2+∠3=90°，因此∠CKF是直角，其對頂角∠LKN也是直角。同理可證∠L、∠M、∠N都是直角，因此KLMN是長方形。...(1)

因為EC=AG且EC//AG，所以ECGA是平行四邊形，因此EA//CG。

因為E是DC的中點且EN//CK，所以DN=NK。...(2)

三角形DCK和三角形CBL，因為∠1=∠2，∠K=∠L=90°，DC=CB，所以三角形DCK和三角形CBL全等(AAS全等性質)。
同理可證直角三角形ADN、直角三角形BAM、直角三角形CBL、直角三角形DCK都全等。

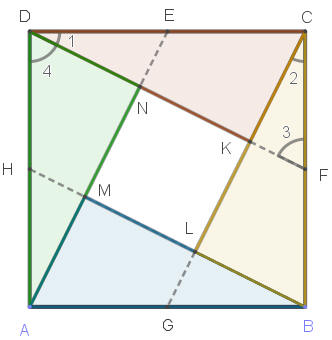
由(2)知直角三角形ADN、直角三角形BAM、直角三角形CBL、直角三角形DCK的兩股比都是2︰1，而且KLMN的四邊長相等，由(1)知KLMN是正方形。因此正方形MNKL、直角三角形ADN、直角三角形BAM、直角三角形CBL、直角三角形DCK的面積比是1︰1︰1︰1︰1︰1。

相關連結︰

■ 正方形等積變換十字形

■ 過正方形中心點，五等分正方形的面積