 |
$1^2+1^2=1\times 2$ |
 |
$1^2+1^2+2^2=2\times 3$ |
 |
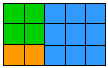$1^2+1^2+2^2+3^2=3\times 5$ |
 |
$1^2+1^2+2^2+3^2+5^2=5\times 8$ |
斐波拉契數列平方和性質
斐波拉契數列 1，1，2，3，5，8，13，21，34，55，89，.......，fn，其中第n項 fn = fn-1 + fn-2。
| |
$1^2+1^2=1\times 2$ |
| |
$1^2+1^2+2^2=2\times 3$ |
| |
$1^2+1^2+2^2+3^2=3\times 5$ |
| |
$1^2+1^2+2^2+3^2+5^2=5\times 8$ |
可以推廣得，$1^2+1^2+2^2+3^2+5^2+8^2+\dots+f_n^2=f_nf_{n+1}$。
|
$f_1=f_2=1$，$f_1^2=f_1f_2$ $f_2=f_3-f_1$，$f_2^2=f_3f_2-f_1f_2$ $f_3=f_4-f_2$，$f_3^2=f_4f_3-f_2f_3$ ......... $f_n=f_{n+1}-f_{n-1}$，$f_n^2=f_nf_{n+1}-f_nf_{n-1}$ |
(1) (2) (3) ...... (n) |
(1)+(2)+(3)+....+(n) 得 $f_1^2+f_2^2+f_3^2+\dots+f_n^2=f_nf_{n+1}$。