費馬點.

費馬點(托里切利點)

如果有一家公司想要選擇一個地點F來成立辦公室，已知公司員工多數居住在地點A、 B、C三個小鎮。如果希望辦公室F點到三個小鎮地點A、 B、C的距離和是最短的，那麼辦公室地點F應該選擇在哪裡?

這一道問題被稱作費瑪點問題，最早發生在1643年，費瑪寫信給義大利托里切利(Torricelli) (氣壓計發明人)討論的問題，最後由托里切利提出解決的方法。

費瑪點問題如下：
「平面上有不共線的三個點，點A、點 B、點C，在同一平面上有點P，P點分別到點A、點 B、點C的距離之和是 PA + PB + PC。那麼是否存一點Q，使得 QA + QB + QC < PA + PB + PC 呢？」也就是說，要找出一定點，該定點到三個頂點的距離和是最小。托里切利解決了這個問題，但是生前並沒有發表，而是由他的學生維維亞尼在1659年代為發表。

可以參閱 geogebra費瑪點，得知費瑪點F連接三角形ABC的三個頂點，三個夾角∠AFB、∠BFC、∠CFA都是120度。

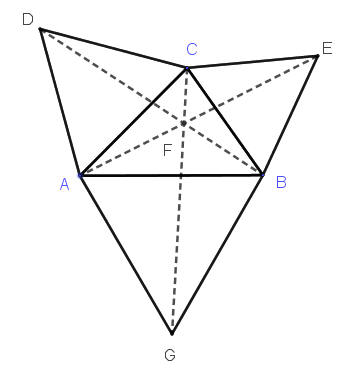
如果$\triangle ABC$沒有內角大於120°，分別以$\triangle ABC$的三個邊向外各做正$\triangle ABG$、正$\triangle BCE$和正$\triangle CAD$。連接線段AE、BD、CG ，只相交於一點F，F點即為費瑪點。