凸槌的結論

數學家華羅庚說過一個故事， 「有一個人買一隻公雞回家，他在第一天餵雞一把米，第二天也餵雞一把米。就這樣一連幾天，每天都餵雞一把米。這隻公雞認為每天都會有一把米可吃，沒料到竟然有親戚來訪，公雞也成為餐桌盤中飧。」華羅庚將這一隻公雞推導結論的思考方法稱為"公雞歸納法"，它是一種不完全歸納法。華羅庚認為不完全歸納法是不可靠的，如果只對部分進行研究就下結論，卻沒經過證明就說結論適用於全部，往往會鬧出笑話來。

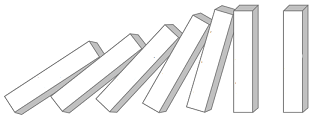
數學歸納法是說，如果有一批編了號碼的數學命題，證明第1號命題是正確，假設第n號命題正確，如果能證明第n+1號命題也是正確的，那麼整批命題就都是正確。如同推倒多米諾骨牌，推倒第一張骨牌，假設第n張骨牌會倒下，如果第n+1張骨牌也會倒下，則所有的骨牌多會倒下。

然而事實上，就算第n號命題是正確，也不一定就能證明出第n+1號命題是正確的。數學史就發生過公雞歸納法的例子，法國數學家Legendre A.M在1798年發表二次函數f(n)=n²+n+41的所有函數值都是質數。可是他錯了，因為f(40)=1681=41² ; f(41)=1763=41×43，顯然f(40)和f(41)都不是質數。事實上，當n ≦ 39，f(n)=n²+n+41的函數值都是質數。

法國數學家Fermat猜想，對於任何自然數n，$2^{2^{n}}+1$都是質數。事實，當n=0、1、2、3、4 時，$2^{2^{n}}+1$ 是質數，但是$2^{2^{5}}+1$=641×6700417並不是質數。

再看一例，$3=2^{0}+2$，$5=2^{1}+3$，$7=2^{2}+3$，$11=2^{3}+3$，$13=2^{3}+5$。是否發現大於2的質數可以表示成2的冪次方和一個質數的相加和。或許你會謹慎地再多找ㄧ些算例，$17=2^{2}+13$，$19=2^{3}+11$，$23=2^{4}+7$，$29=2^{4}+13$，$31=2^{3}+23$，$37=2^{3}+29$，$41=2^{2}+37$，$43=2^{5}+11$，....，$113=2^{4}+97$。到此，你可能會大膽下一個猜想︰「大於2的質數可以表示成2的冪次方和一個質數的相加和。」

可是這猜想錯誤，下一個質數127就出現矛盾。因為

$127=2^{1}+5^{3}=2^{2}+3\times41=2^{3}+7\times17=2^{4}+3\times37=2^{5}+5\times19=2^{6}+3^{2}\times7$。