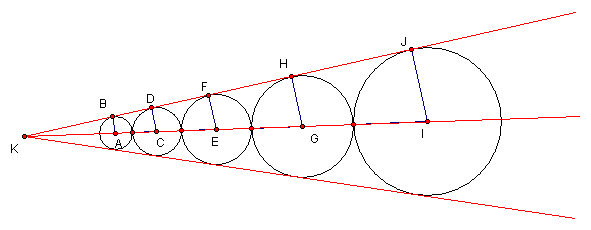
共外公線的連續外切圓

如圖，∠K內圓A、圓C、圓E、圓G、圓I都和∠K兩夾邊相切，而且相鄰的兩圓都外切。如果圓A、圓C、圓E、圓G、圓I的半徑分別是r₁、r₂、r₃、r₄、r₅_，則

(1) r₁、r₂、r₃、r₄、r₅成等比數列。

(2) 外切長BD、DF、FH成等比數列。

(1)

假設圓A、圓C、圓E的半徑分別是 r₁、r₂、r₃，

過A點作AM //BF，

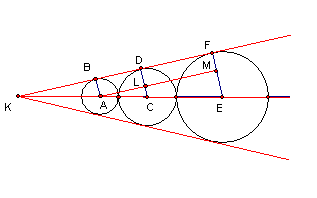
則AE：AC = EM：CL，即

( r₁+r₂+r₂+r₃)：( r₁+r₂) =( r₃ -r₁)：( r₂ - r₁)

因此 $\large\frac{(r_1+r_2)+r_2+r_3}{r_1+r_2}$=$\large\frac{r_3-r_1}{r_2-r_1}$，

即1+$\large\frac{r_2+r_3}{r_1+r_2}$=$\large\frac{r_3-r_1}{r_2-r_1}$。

因為$\large\frac{r_2+r_3}{r_1+r_2}$=$\large\frac{r_3-r_1}{r_2-r_1}$-1=$\large\frac{(r_3-r_1)-(r_2-r_1)}{r_2-r_1}$=$\large\frac{r_3-r_2}{r_2-r_1}$，因此

(r₂+r₃)(r₂-r₁)=(r₁+r₂)(r₃-r₂)，得(r₂)²=r₁r₃。

所以 r₁、r₂、r₃成等比數列，同理可知r₁、r₂、r₃、r₄、r₅成等比數列。

(2)

圓A、圓C、圓E、圓G的半徑分別是 r₁、r₂、r₃、r₄。

因為 BD²= 4 r₁r_2，DF²= 4 r₂r_3，FH²= 4 r₃r_4，

所以 BD² ×FH² = (4r₁r_2₎(4r₃r₄) =16(r₁r₃)(r₂r₄)= 16(r₂)²(r₃)² = (4 r₂r₃)²=( DF²)²，

即 BD× FH= DF²，因此 BD 、DF、FH成等比數列。