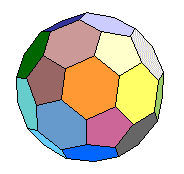
多面體Euler's 公式

多面體的頂點數( number of vertices)=V ，邊數(number of edges)=E ，面數(number of faces)=F

，則 V - E + F = 2。

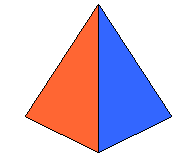
正四面體(Tetrahedron) V=4，E=6，F=4， 4 - 6 + 4 = 2
正六面體(Cube) V=8，E=12，F=6， 8 - 12 + 6 = 2
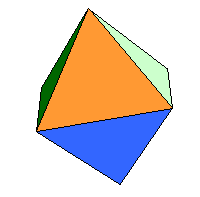
正八面體(Octahedron) V=6，E=12，F=8， 6 - 12 + 8 = 2
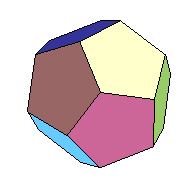
正十二面體(Dodecahedron) V=20，E=30，F=12，20 - 30 + 12 = 2
正二十面體(Icosahedron) V=12，E=30，F=20，12 - 30 + 20 = 2

以上5種正多面體，也稱作柏拉圖多面體，每一種正多面體的面是全等的正多邊形。

若有二種或二種以上的全等正多邊形的對稱多面體，稱作阿基米得多面體，例如：

巴克球(Buckyball)，C₆₀的分子結構就是巴克球，其中

V=60，E=90，F = 32 (含12個正五邊形和 20個正六邊形)，60 - 90 + 32 = 2

足球近似巴克球，有12片黑色正五邊形球皮，20片白色正六邊形球皮。

許多病毒是正20面體(icosahedron)，例如皰疹(herpes)病毒、水痘(chickenpox)病毒 、人體疣(human wart)病毒、犬類傳染性肝炎病毒、腺病毒(adenovirus)等。

Copyright © 昌爸工作坊 all rights reserved.