可以尺規作圖三等分的最小整數角度

1837年法國數學家 Pierre Wantzel (1814–1848) 利用迦羅瓦的理論證明尺規作圖三等分任意角是不可能的。

尺規作圖要求在有限的步驟內完成作圖，如果沒有這個限制，則經過無窮次數的四等分已知角，理論上可趨近於三等分角。

因為$\dfrac{1}{4}$+$(\dfrac{1}{4})^2$+$(\dfrac{1}{4})^3$+....=$\dfrac{\dfrac{1}{4}}{1-\dfrac{1}{4}}$=$\dfrac{1}{3}$。

雖然尺規作圖三等分任意角是不可能的，但是有一些角是可以尺規作圖三等分，那麼可以尺規作圖三等分的最小整數角度是多少?

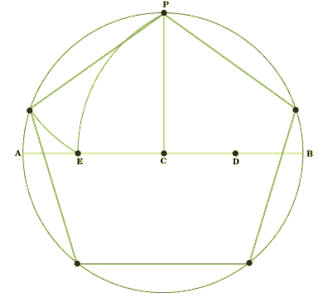
可以尺規作圖正五邊形

畫一圓 C。

作直徑AB。

作BC的中點D。

過C點作AB的垂直線交圓C於P點。

以D點為圓心，DP為半徑畫弧交AB於E點。

以P點為圓心，PE為半徑畫弧交圓於一點。再連續取四個等弧，連接交點，就可以作出正五邊形。

正五邊形的邊和對角線夾36度，可以尺規作圖30度角，得6度角，再尺規作圖平分角得3度角。

而3度角的3倍是9度角，因此尺規作圖三等分的最小整數角度是9度，也就是說「角度是9的倍數，這樣的角可以尺規作圖三等分」。