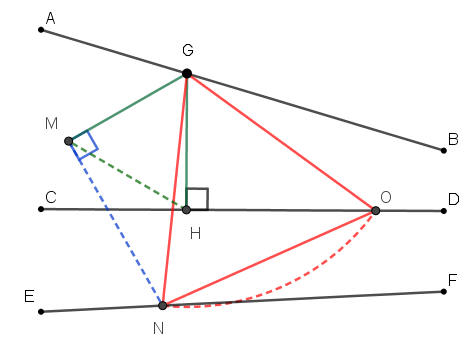
在三線上尺規作正三角形(頂點在不同線上)

已知︰直線AB、直線CD、直線EF，不一定兩兩平行。試尺規作正三角形，頂點位在不同的直線上。

1. 在直線AB上取一點G。

2. 過G點作直線CD的垂直線，並和直線CD相交於H點。

3. 以GH為邊作正三角形GHM。

4. 過M點作MG的垂直線MN，並和直線EF相交於N點。

5. 以G點為圓心，GN為半徑畫弧，此弧和直線CD相交於O點。

6. 三角形GNO即為所求。
   
   

說明

直角三角形GMN和直角三角形GHO，GN=GO且GM=GH，根據斜股性質知直角三角形GMN和直角三角形GHO全等，

因此∠MGN=∠HGO。

因為正三角形GHM，∠MGN+∠NGH=60°，所以∠HGO+∠NGH=60°，即∠NGO=60°。

因為GN=GO且∠NGO=60°，所以三角形GNO是正三角形。

相關連結︰作正三角形，三頂點分別在三直線 (ggb)