Processing math: 100%

三角函數的差化積公式

  1.  sin α-sin β=2 sinα−β2 cosα+β2

  2.  cos α-cos β=-2 sinα−β2 sinα+β2

 

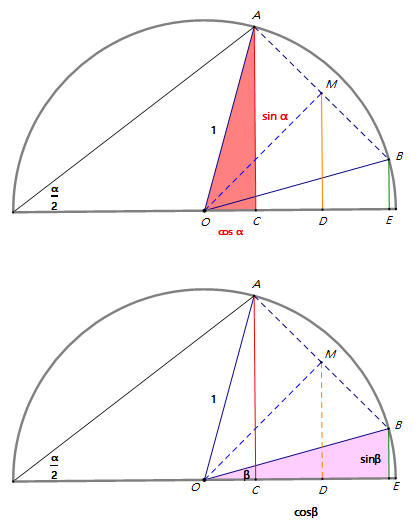
半圓半徑OA=1，∠AOE=α，∠BOE=β，OM垂直平分AB，AC⊥OE，MD⊥OE，BE⊥OE。
 AC=sinα，OC=cos α；BE=sin β，OE=cos β。

 

 

OM平分∠AOB，∠MOB=α−β2。∠MAC==∠MOE=α−β2+β=α+β2。
 BF⊥AC交MD於N點；AF=AC-FC=AC-BE=sin α-sin β。
MN=AF2=sin α−sin β2。

 

 

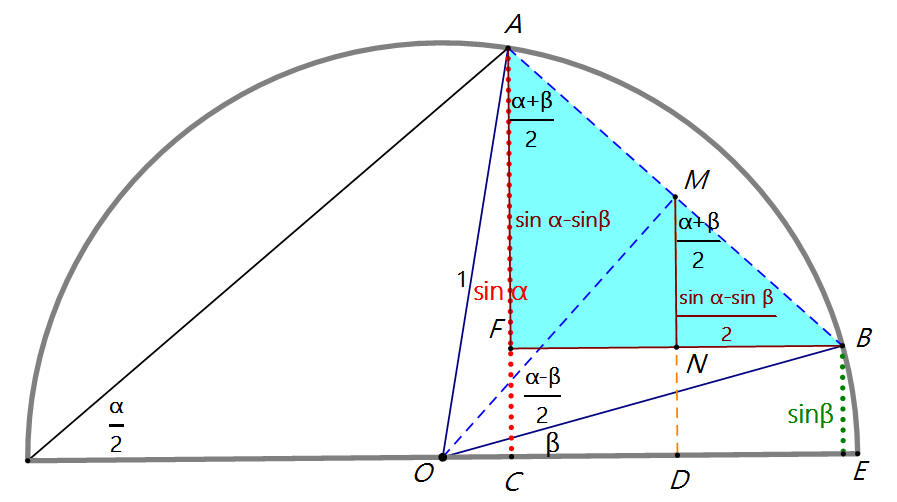
MB= MA=sin α− β2 。∠BMN=α+β2。MN=sin α− β2 × cos α+ β2 。

所以sin α−sin β2=sin α− β2 × cos α+ β2，得

 sin α-sin β==2 sin α− β2  cos α+ β2。 ... (1)

 

 

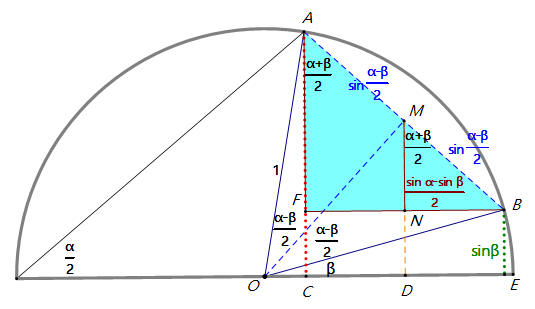
NB=sin α− β2 × sin α+ β2=DE

因為D是CE的中點，DE=¯OE−¯OC2=cos β−cos α2。 

所以cos β−cos α2=sin α− β2 × sin α+ β2，得

 cos β-cos α=2sin α− β2  sin α+ β2;

 cos α-cos β= -2sin α− β2  sin α+ β2。 ... (2)

 

 

 

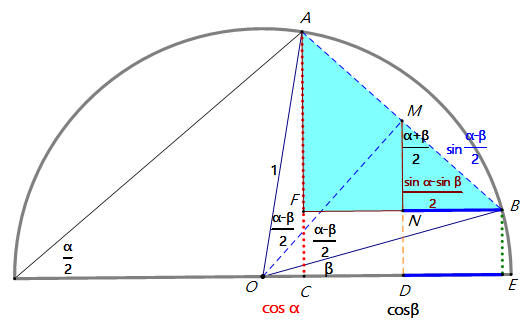
由以上圖解可知

  1.  sin α-sin β=2 sinα−β2 cosα+β2

  2.  cos α-cos β=-2 sinα−β2 sinα+β2


Copyright ©昌爸工作坊 all rights reserved.