裁切組合正方形

「兩個不同的正方形，裁切一個正方形，是否可以和另一個正方形組合成正方形呢？」

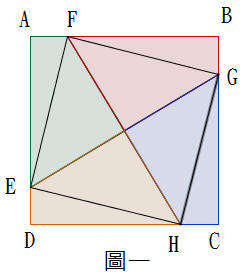
如果兩個正方型的邊長分別是a和b，其中a ≧ b。圖一，在邊長a的正方形ABCD的四個邊上分別取E點、F點、G點、H點，使得AF=BG=CH=DE，則可證明△AFE、△BGF、△CHG、△DEH是四個全等的直角三角形。
也可以證明四邊形EFGH是正方形，因此EG=FH，且EG和FH互相垂直平分。

如果順著EG和FH裁切，正方形ABCD會被分成四個全等的四邊形，他們都各自擁有一組直角的對角。

△AFE、△BGF、△CHG、△DEH四個直角三角形都全等，令其兩股差都是b。
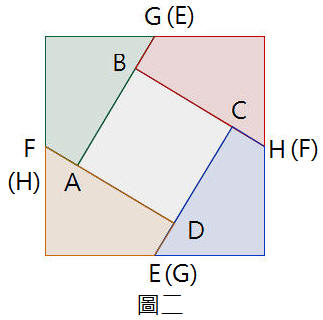
圖二，中空四邊形的邊長AB=AE-BG=AE-AF=b，同理BC=CD=DA=b。又A、B、C、D四個角都是直角，所以中空四邊形是邊長b的正方形。

因為AE-ED=b，且AE+ED=a，所以AE=$\large\frac{a+b}{2}$，ED=$\large\frac{a-b}{2}$。

綜合上述，如果兩個正方形其邊長分別是a和b，則取AF=BG=CH=DE=$\large\frac{a-b}{2}$，並順著EG和FH剪裁，再拼貼成圖二，則中空正方形的邊長是b。

所以「兩個不同的正方形，裁切一個正方形，可以和另一個正方形組合成正方形。」
利用相同方法，可以將n個正方形組成一個正方形。

相關連結︰正方形二合一 (ggb)