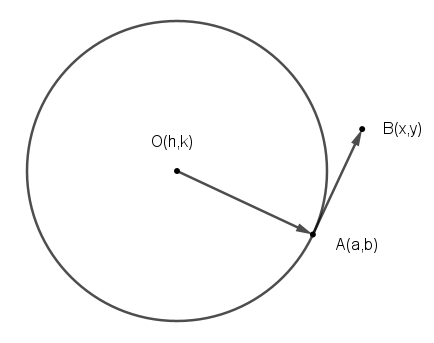
過圓上一點的切線方程式
「 已知圓心(h,k),圓上一點A(a,b),則過A點的切線方程式是 (a-h)(x-h)+(b-k)(y-k)=(a-h)2+(b-k)2。」
令圓的半徑 r,則 r2=(a-h)2+(b-k)2。圓的方程式是 (x-h)2+(y-k)2=r2。
說明1,利用斜率
過(h,k)和(a,b)兩點的直線斜率是b−ka−h。過A點的切線斜率和b−ka−h的乘積是-1,所以過A點的切線斜率是h−ab−k。
因此過A點的切線的方程式是 y-b=h−ab−k(x-a),
(y−b)(b−k)=(x−a)(h−a),
(y−b−k+k)(b−k)=(x−a−h+h)(h−a),
[(y−k)+(k−b)](b−k)=[(x−h)−(a−h)][−(a−h)],
(y−k)(b−k)−(b−k)2=−(x−h)(a−h)+(a−h)2,
(a−h)(x−h)+(b−k)(y−k)=(a−h)2+(b−k)2=r2。
說明2,利用向量內積
→OA⊥→AB
(a−h,b−k)⋅(x−a,y−b)=0
(a−h)(x−a)+(b−k)(y−b)=0
循說明1的運算式得 (a−h)(x−h)+(b−k)(y−k)=(a−h)2+(b−k)2=r2。

例如,已知圓心(3,4),圓上一點A(7,9),則過A點的切線方程式是(7-3)(x-3)+(9-4)(y-4)=(7-3)2+(9-4)2,即 4x+5y=73。
或是用內積是0求切線方程式會比較快,(7-3,9-4)‧(x-7,y-9)=0,4x-28+5y-45=0,4x+5y=73。
Copyright © 昌爸工作坊(數學網站) All Rights Reserved.