$cos \theta \approx1-\dfrac{\theta^2}{2}$  (當θ趨近於0)

這裡角度單位採弳度(弧度，rad)

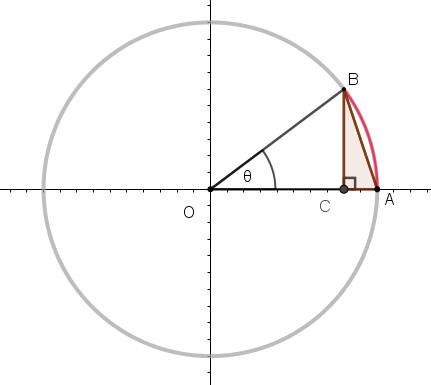
如果圓O半徑是1，且∠BOA=θ，BC⊥OA，垂直是C點，

則OC=OB cosθ，BC=OB sinθ，因此 CA=1-OC=1-OB cosθ。

直角三角形BAC，BA²=BC²+ CA² =( OB sinθ )² +( 1-OB cosθ )² = 2 -2 OB cosθ =2 - 2 cosθ。

因為 $\overset{\LARGE{\frown}}{AB}=\overline{AO}\cdot\theta$，所以 $\overset{\LARGE{\frown}}{AB}=\theta$

當θ趨近於0時，$\overline{AB}=\overset{\LARGE{\frown}}{AB}$，因此θ²=2 - 2 cosθ，即

$cos \theta \approx1-\dfrac{\theta^2}{2}$。

因為$sin^2\theta+cos^2\theta=1$，所以$sin\theta=\sqrt{1-cos^2\theta}$。因此，當θ趨近於0時，

$\sin\theta\approx\sqrt{1-(1-\dfrac{\theta^2}{2})^2}=\sqrt{\theta^2-\dfrac{\theta^4}{4}}\approx\theta$

Copyright © 昌爸工作坊 all rights reserved.