圖解柯西不等式

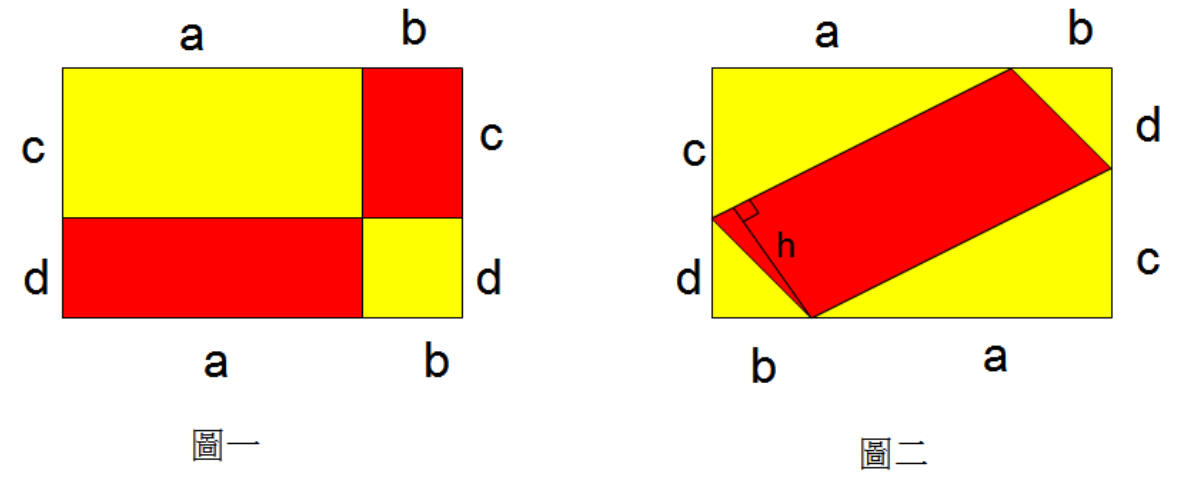
圖一和圖二是全等的長方形，圖一黃色區域的面積是ac+bd，圖二黃色區域的面積=(½)ac×2+(½)bd×2=ac+bd。

因為圖一和圖二的黃色區域面積大小相等，所以圖一和圖二的紅色區域面積大小也應該是相等的。

因為圖一紅色區域面積是ad+bc，因此圖二的紅色區域(平行四邊形)面積 = ad+bc=× h。......(1)

(一)、如果圖二紅色區域不是長方形，

因為直角三角形的斜邊長大於股長，所以 > h。......(2)

綜合(1)(2)可知× > × h = ad+bc，因此× > ad + bc，即 (a²+c²)(d²+b²) > (ad+bc)² 。

(二)、如果圖二紅色區域是長方形，則 h=，由(1)可知 ad+bc =×，即 (ad+bc)² = (a²+c²)(d²+b²)。

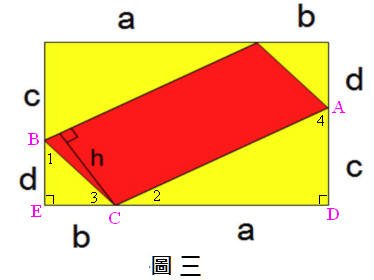
如圖三，如果 a：d = c：b，則紅色區域一定是長方形，理由如下：

因為直角△CDA和直角△BEC，a：d = c：b 即 CD : BE = DA : EC ，又∠D =∠E = 90∘，所以 △CDA和直角△BEC相似 (SAS相似)，因此 ∠1=∠2。因為∠1+∠3 = 90∘，所以∠2+∠3 = 90，可知∠BCA是直角，因此圖三的紅色區域(平行四邊形)是長方形。

由上述可知如果 a：d = c：b，則 (a²+c²)(d²+b²) = (ad+bc)² 。

可以推廣得知，「若 a、b、c、d是任意數，則(a²+c²)(d²+b²) ≧ (ad+bc)² ，當 a：d = c：b 時，等號成立。」