猜出號碼牌總和

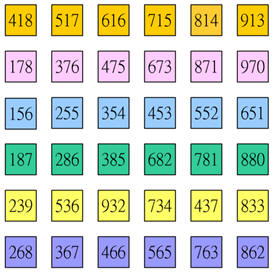
有六種不同顏色的號碼牌，每一種顏色的號碼牌有 6 張，每一張號碼牌有一個三位數。

任意挑選出6張不同顏色的號碼牌，計算這6個三位數的個位數的總和N。你只要正確說出N，則一定可以速算出這6個三位數的相加總和? 如何做，為什麼?

仔細觀察後發現在相同顏色的號碼牌上的三位數的十位數字是相同的，並且其百位數和個位數相加和是相同的。例如每張黃色號碼牌的三位數的十位數字都是3，其百位數和個位數相加和都是11。

附圖的號碼牌由上而下每一列的三位數的十位數分別是1、7、5、8、3、6。三位數的百位數和個位數相加和分別是12、9、7、8、11、10。
如果選出的 6 張不同顏色的號碼牌上的三位數的個位數字分別是 a、b、c、d、e、f，則三位數的百位數字分別是12-a、9-b、7-c、8-d、11-e、10-f。

因此這6個三位數相加和等於
100[(12-a)+(9-b)+(7-c)+(8-d)+(11-e)+(10-f)]+10(1+7+5+8+3+6)+( a+b+c+d+e+f )＝
100[57-( a+b+c+d+e+f )]+300+( a+b+c+d+e+f )＝

100[57-( a+b+c+d+e+f )+3]+( a+b+c+d+e+f )＝
100[60-( a+b+c+d+e+f )]+( a+b+c+d+e+f )=100(60-N)+N，其中N=a+b+c+d+e+f ，即6個三位數的個位數字和。