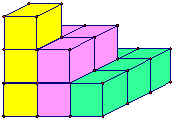
堆疊積木求級數平方和

使用相同的正方體積木一層層堆疊成金字塔狀，每一層鳥瞰都是正方形，所使用的積木個數是平方數。

由最上一層計算積木個數直到最後一層，第一層有1塊，第二層有4塊，第三層有9塊，積木總共有 1²+2²+3² (塊) ...(1)。

每一層如下，

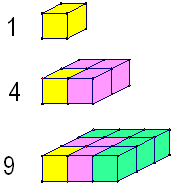
3層都有，每一層有1個積木，總共有1×3=3(個)，

2層有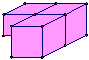，每一層有3個積木，個數有3×2=6(個)，

只有一層有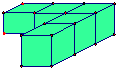，這一層有5個積木，個數有5×1=5(個)。

三層積木總數=1×3+3×2+5×1 ....(2)，
由(1)(2)得知 1²+2²+3²=1×3+3×2+5×1。

推廣得

1²+2²+3²+4²+...........+(n-1)²+n²=

1×n+3×(n-1)+5×(n-2)+7×(n-3)+....+(2n-5)×3+(2n-3)×2+(2n-1)×1=

(2n-1)×1++(2n-3)×2+(2n-5)×3+....+7×(n-3)+5×(n-2)+3×(n-1)+1×n=

$$\sum_{m=1}^{n}(2n-(2m-1))m=2n\sum_{m=1}^{n}m-2\sum_{m=1}^{n}m^{2}+\sum_{m=1}^{n}m$$

所以 $$\sum_{m=1}^{n}m^{2}=2n\sum_{m=1}^{n}m-2\sum_{m=1}^{n}m^{2}+\sum_{m=1}^{n}m$$
因此 $$3\sum_{m=1}^{n}m^{2}=2n\sum_{m=1}^{n}m+\sum_{m=1}^{n}m=(2n+1)\frac{n(1+n)}{2}$$

得$$\sum_{m=1}^{n}m^{2}=\frac{n(n+1)(2n+1)}{6}$$